
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() ,下列结论:①△APD≌△AEB;②点B到直线AE的距离为
,下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=
;③EB⊥ED;④S△APD+S△APB=![]() .其中正确结论的序号是_____.
.其中正确结论的序号是_____.
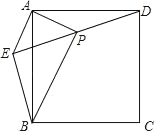
【答案】①③④
【解析】
作BF⊥AE于F,根据正方形的性质证明△APD≌△AEB即可判断①,根据△AEP为等腰直角三角形,得到∠APD=135°,再求出∠PEB=90°,即可判断③,根据Rt△PED中,求出BE=![]() ,再求出△BEF为等腰直角三角形,利用BF=
,再求出△BEF为等腰直角三角形,利用BF=![]() BE即可求出BF即可判断②,再根据S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE即可求出④的正确性.
BE即可求出BF即可判断②,再根据S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE即可求出④的正确性.
解:作BF⊥AE于F,如图,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵AP⊥AE,
∴∠EAP=90°,即∠2+∠3=90°,
∵∠1+∠2=90°,
∴∠1=∠3,
在△APD和△AEB中
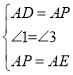 ,
,
∴△APD≌△AEB,所以①正确;
∵AE=AP,∠PAE=90°,
∴△AEP为等腰直角三角形,
∴∠4=∠5=45°,
∴∠APD=135°,
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠PEB=135°﹣∠4=90°,
∴BE⊥ED,所以③正确;
在Rt△PED中,BE=![]() ,
,
在Rt△BEF中,∵∠BEF=180°﹣∠AEB=45°,
∴△BEF为等腰直角三角形,
∴BF=![]() BE=
BE=![]() ×
×![]() =
=![]() ,所以②错误;
,所以②错误;
∵△APD≌△AEB,
∴S△APD=S△AEB,
∴S△APD+S△APB=S△AEB+S△APB=S四边形AEBP=S△AEP+S△PBE=![]() ×1×1+
×1×1+![]() ×
×![]() ×
×![]() =
=![]() ,所以④正确.
,所以④正确.
故答案为①③④.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.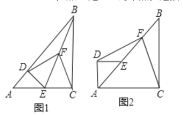
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,以A为圆心,AB长为半径作弧BE,CD于E,若AB=4,则阴影部分的面积为_____(结果保留π和根号).
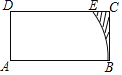
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB⊥AC,过点D作DE⊥AD交直线AC于点E,点O是对角线AC的中点,点F是线段AD上一点,连接FO并延长交BC于点G.
(1)如图1,若AC=4,cos∠CAD=![]() ,求△ADE的面积;
,求△ADE的面积;
(2)如图2,点H为DC是延长线上一点,连接HF,若∠H=30°,DE=BG,求证:DH=CE+![]() FH.
FH.
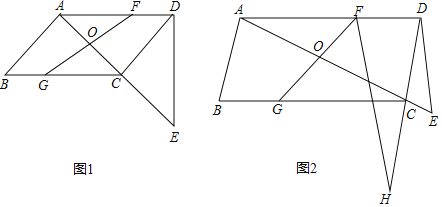
查看答案和解析>>
科目:初中数学 来源: 题型:
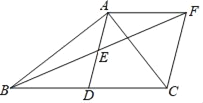
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的情况下,点M在AC线段上移动,请直接回答,当点M移动到什么位置时,MB+MD有最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
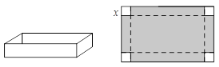
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
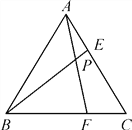
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com