
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 上的动点,且
上的动点,且![]() .
.
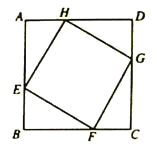
(1)求证:四边形![]() 是正方形;
是正方形;
(2)求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)详见解析;(2)四边形![]() 面积的最小值为32.
面积的最小值为32.
【解析】
(1)由正方形的性质得出.∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,
∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;
(2)设四边形EFGH面积为S,AE=xcm,则BE=(8-x)cm,由勾股定理得出S=x2+(8-x)2=2(x-4)2+32,S是x的二次函数,容易得出四边形EFGH面积的最小值.
证明:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是正方形.
是正方形.
(2)设![]() ,
,
则![]() ,
,
S四边形EFGH![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 面积的最小值为32.
面积的最小值为32.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.

(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=![]() ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DFGF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是矩形
是矩形![]() 内的任意一点,连接
内的任意一点,连接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() ,
,![]() , 给出如下结论:①
, 给出如下结论:①![]() ②
②![]() ③若
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]() 点在矩形的对角线上.其中正确的结论的序号是( )
点在矩形的对角线上.其中正确的结论的序号是( )

A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点A,沿顺时针方向旋转后得到Rt△AB1C1,当点B1恰好落在斜边BC的中点时,则∠B1AC=( )

A.25°B.30°C.40°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚质地均匀的正四面体骰子,骰子各个面的点数分别是1至4的整数,把这两枚骰子向下的面的点数记为(a,b),其中第一枚骰子的点数记为a,第二枚骰子的点数记为b.
(1)用列举法或树状图法求(a,b)的结果有多少种?
(2)求方程x2+bx+a=0有实数解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com