
����Ŀ����ͼ���ס�����������ת����Ϸʱ������������������ת����ת��A��B��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿһ�������ڱ������֣���Ϸ����ͬʱת������ת�̣���ת��ֹͣ��ָ����ָ���������֮��Ϊ0ʱ����ʤ������֮��Ϊ1ʱ���һ�ʤ�����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ��
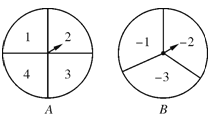
��1���û���״ͼ���б������һ�ʤ�ĸ��ʣ�
��2�������Ϸ����Լס���˫����ƽ�����жϲ�˵�����ɣ�
 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��Բ���������______��
��2����ͼ��AB�ǡ�O���ң�AB��8����C�ǡ�O�ϵ�һ�����㣬�ҡ�ACB��45��������M��N�ֱ���AB��AC���е㣬��MN���ȵ����ֵ��_____��
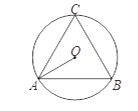
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���Ȼ�������ֵ��![]() ���У�a�Ƿ���x2+3x+1��0�ĸ���
���У�a�Ƿ���x2+3x+1��0�ĸ���
��2����֪������y��ax2+bx+c�ĶԳ���Ϊx��2���Ҿ����㣨1��4���ͣ�5��0��������������ߵı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
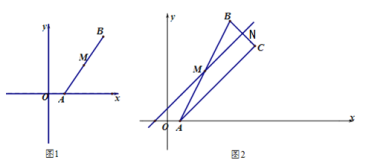
����Ŀ�����壺��ƽ��ֱ������ϵ�У��ѵ�������ƽ��1����λ��������ƽ��2����λ��ƽ�Ƴ�Ϊһ��бƽ�ƣ���֪��A��1��0������A����n��бƽ�Ƶõ���B����M���߶�AB���е㣮
��1����n=3ʱ����B�������� ����M�������� ��
��2����ͼ1������M����![]() ��ͼ���ϣ���n��ֵ��
��ͼ���ϣ���n��ֵ��
��3����ͼ2������M����ֱ��![]() ������C�ǵ�B����ֱ��
������C�ǵ�B����ֱ��![]() �ĶԳƵ㣬BC��ֱ��
�ĶԳƵ㣬BC��ֱ��![]() �ཻ�ڵ�N��
�ཻ�ڵ�N��
����֤����ABC��ֱ��������
�ڵ���C������Ϊ��5��3��ʱ����MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD���ı���CEFG���Ǿ��Σ���E��G�ֱ��ڱ�CD��CB�ϣ���F��AC�ϣ�AB��3��BC��4
��1����![]() ��ֵ��
��ֵ��
��2���Ѿ���CEFG�Ƶ�C˳ʱ����ת��ͼ����λ�ã�PΪAF��BG�Ľ��㣬����CP
������![]() ��ֵ��
��ֵ��
�����ж�CP��AF��λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
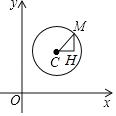
����Ŀ����ƽ��ֱ������ϵ�У���C��x0��y0��ΪԲ�İ뾶Ϊr��Բ�ı������ǣ�x��x0��2+��y��y0��2��r2�����磬��ƽ��ֱ������ϵ�У���C��Բ��C��2��3������M��3��5����Բ��һ�㣬��ͼ������C����M�ֱ���x�ᡢy���ƽ���ߣ����ڵ�H����Rt��MCH�У��ɹ��ɶ����ɵã�r2��MC2��CH2+MH2��1+4��5����ԲC�ı������ǣ�x��2��2+��y��3��2��5����ô�Ե㣨��3��4��ΪԲ�ģ����㣨��2����1����Բ�ı�������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һֻֽ����װ�г���ɫ����ȫ��ͬ�ĺ�ɫ����ɫ����ɫƹ����100������ֽ������������һ��������ɫ��ɫ��ĸ��ʷֱ���0.2��0.3��
��1�������ֽ������ɫ��ĸ�����
��2��С����ֽ�����ٷŽ���ɫ�����ɸ���С��Ϊ�˹��Ʒ���ĺ���ĸ����������������������Ⱥ�����������һ���������ɫ���ٰ����Ż������У�����ظ��������̺����������������Ƶ����0.5������������ݴ˹���С������ĺ���ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������ͼ�٣���A��ֱ��MN�ϣ���B��ֱ��MN�⣬����AB�����߶�AB���е�P��PC��MN������MAB��ƽ����AD�ڵ�C������BC����֤��BC��AD��
Ӧ�ã���ͼ�ڣ���B�ڡ�MAN�ڲ�������AB�����߶�AB���е�P��PC��AM������MAB��ƽ����AD�ڵ�C����PE��AN������NAB��ƽ����AF�ڵ�E������BC��BE������MAN��150�������CBE�Ĵ�СΪ______�ȣ�
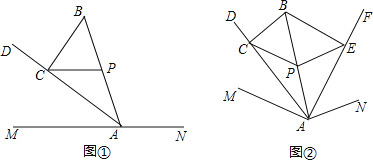
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ��һԪ���κ���
��һԪ���κ���![]() ��
��![]() ����ͼ����
����ͼ����![]() ���ཻ��
���ཻ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
�� ���һԪ���κ����Ĺ�ϵʽ��
�� ��![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ��
��![]() ��Ĵ���
��Ĵ���![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
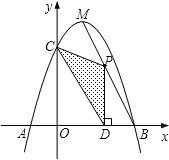
�� ̽���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊֱ�������Σ�������ڣ����
Ϊֱ�������Σ�������ڣ����![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com