
【题目】定义:在平面直角坐标系中,把点先向右平移1个单位,再向上平移2个单位的平移称为一次斜平移.已知点A(1,0),点A经过n次斜平移得到点B,点M是线段AB的中点.
(1)当n=3时,点B的坐标是 ,点M的坐标是 ;
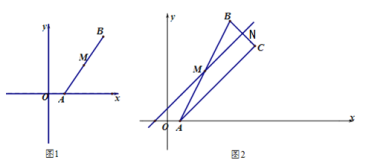
(2)如图1,当点M落在![]() 的图像上,求n的值;
的图像上,求n的值;
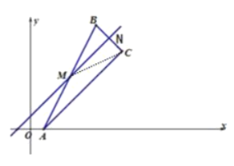
(3)如图2,当点M落在直线![]() 上,点C是点B关于直线
上,点C是点B关于直线![]() 的对称点,BC与直线
的对称点,BC与直线![]() 相交于点N.
相交于点N.
①求证:△ABC是直角三角形
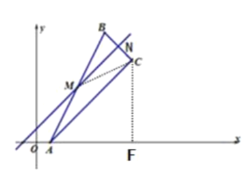
②当点C的坐标为(5,3)时,求MN的长.
【答案】(1)![]() ,
,![]() ;(2)2;(3)①详见解析;②
;(2)2;(3)①详见解析;②![]()
【解析】
(1)由题中斜平移及中点公式即可求得;
(2)根据定义,表达出点M的坐标,再代入反比例函数中计算即可;
(3)①根据中心对称及轴对称得到![]() ,再由等腰三角形的性质进行角度运算得出
,再由等腰三角形的性质进行角度运算得出![]() 即可证明;
即可证明;
②由平行得出△BMN∽△BAC,再根据比例关系得出MN的长度即可.
解:(1)当n=3时,点A(1,0)向右平移3个单位,向上平移6个单位得到点B,
∴点B![]() ,
,
由中点公式可得![]() ,
,![]() ,
,
∴点M![]() ,
,
故答案为:![]() ,
,![]()
(2)由定义可知B(n+1,2n),
∴点M![]() ,
,
∴当点M在![]() 上时,
上时,
有![]() ,
,
解得![]() ,
,
∵n>0,
∴![]()
(3)①连接![]() ,如图:
,如图:
由中心对称可知![]() ,
,
由轴对称可知![]() ,
,
∴![]()
∴![]() ,
,![]()
![]() ,
,
![]()
![]()
![]() 是直角三角形;
是直角三角形;
②过![]() 点作
点作![]() 于点
于点![]() ,如图:
,如图:
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 在直角三角形
在直角三角形![]() 中,
中,![]()
![]()
∴△BMN∽△BAC
![]()
![]()
![]()
![]()


科目:初中数学 来源: 题型:
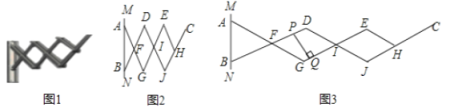
【题目】如图1是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图.![]() 为衣架的墙体固定端,
为衣架的墙体固定端,![]() 为固定支点,
为固定支点,![]() 为滑动支点,四边形
为滑动支点,四边形![]() 和四边形
和四边形![]() 是菱形,且
是菱形,且![]() .点
.点![]() 在
在![]() 上滑动时,衣架外延钢体发生角度形变,其外延长度(点
上滑动时,衣架外延钢体发生角度形变,其外延长度(点![]() 和点
和点![]() 间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42
间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42![]() .当点
.当点![]()
![]() 向点
向点![]() 移动8
移动8![]() 时,外延长度为9
时,外延长度为9![]() .如图3,当外延长度为120
.如图3,当外延长度为120![]() 时,则
时,则![]() 和
和![]() 的间距
的间距![]() 长为_______.
长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
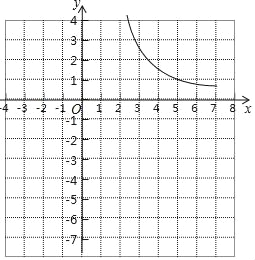
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
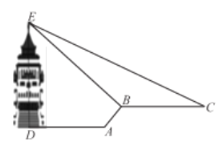
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
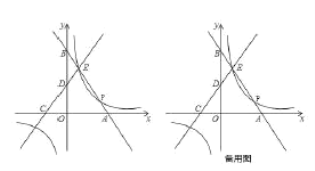
【题目】如图,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 相交于点
相交于点![]() ,线段
,线段![]() 、
、![]() 的长是-元二次方程
的长是-元二次方程![]() 的两根(
的两根(![]() ),
), ![]() ,点
,点![]() 的横坐标为3,反比例函数
的横坐标为3,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)若直线![]() 与反比例函数图象上除点
与反比例函数图象上除点![]() 外的另一交点为
外的另一交点为![]() ,求
,求![]() 的面积:若点
的面积:若点![]() 在
在![]() 轴上,若点
轴上,若点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值:
的最小值:
(2)若点![]() 在坐标轴.上,在平面内存在一点
在坐标轴.上,在平面内存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形且线段
为顶点的四边形是矩形且线段![]() 为矩形的一条边, 直接写出符合条件的
为矩形的一条边, 直接写出符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
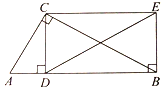
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D ,BE⊥AB,垂足为B,BE=CD连接CE,DE.
(1)求证:四边形CDBE是矩形
(2)若AC=2 ,∠ABC=30°,求DE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
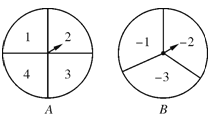
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则OA2﹣AB2=_____.
在第一象限的图象经过点B,则OA2﹣AB2=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
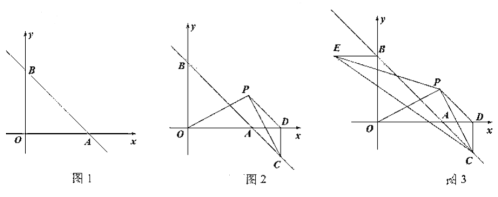
(1)如图1,求直线![]() 的解析式;
的解析式;
(2)如图2,点![]() 在第一象限内,连接
在第一象限内,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的而积为S,求S与
的而积为S,求S与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com