
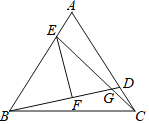
【题目】如图,在等边三角形ABC中,AE=CD,CE与BD相交于点G,EF⊥BD于点F,若EF=4,则EG的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 8
D. 8
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线y=x2+bx+c的表达式;
(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
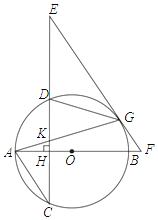
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)扬州市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有__________种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种主案用![]() 、…或①、②、③、…等符号来代表可简化解答过程)
、…或①、②、③、…等符号来代表可简化解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
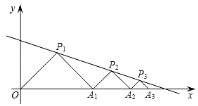
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线![]() 上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,依据图形所反映的规律,Sn=_____.
上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…,依据图形所反映的规律,Sn=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 .
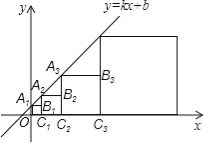
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点A在格点上,B是小正方形边的中点,
的顶点A在格点上,B是小正方形边的中点,![]() ,
,![]() ,经过点A,B的圆的圆心在边AC上.
,经过点A,B的圆的圆心在边AC上.
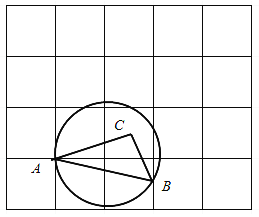
(Ⅰ)线段AB的长等于_______________;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,画出一个点P,使其满足![]() ,并简要说明点P的位置是如何找到的(不要求证明)_____.
,并简要说明点P的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com