
【题目】在△ABC中,AB,BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A.点O在AC的垂直平分线上
B.△AOB,△BOC,△COA都是等腰三角形
C.∠OAB+∠OBC+∠OCA=90°
D.点O到AB,BC,CA的距离相等
【答案】D
【解析】解:A、连接AO、BO、CO,
∵AB、BC的垂直平分线相交于三角形内一点O,
∴AO=BO,BO=CO,
∴AO=CO,
∴点O在AC的垂直平分线上,
所以选项A正确;
B、∵AO=BO,BO=CO,AO=CO,
∴△AOB、△BOC、△COA都是等腰三角形,
所以选项B正确;
C、∵AO=BO,BO=CO,AO=CO,
∴∠OAB=∠ABO,∠OBC=∠OCB,∠OAC=∠OCA,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠OAB+∠OBC+∠OCA=90°,
故选项C正确;
D、∵点O是三边垂直平分线的交点,
∴OA=OB=OC,
但点O到AB、BC、CA的距离不一定相等;
所以选项D错误;
本题选择错误的,
故选D.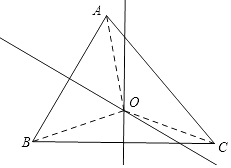
根据垂直平分线的性质得:O也是AC垂直平分线上的点,则O到三个顶点的距离相等,可以得△AOB、△BOC、△COA都是等腰三角形,且根据等边对等角得:∠OAB=∠ABO,∠OBC=∠OCB,∠OAC=∠OCA,再由三角形内角和定理得:∠OAB+∠OBC+∠OCA=90°;
三角形的角平分线的交点到三边的距离相等.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 边上的动点(不含端点),且
边上的动点(不含端点),且![]() 、
、![]() 均过正方形的中心
均过正方形的中心![]() .
.
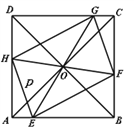
(1)填空: ![]()
![]() (“>”、“<”、“=”);
(“>”、“<”、“=”);
(2)当四边形![]() 为矩形时,请问线段
为矩形时,请问线段![]() 与
与![]() 应满足什么数量关系;
应满足什么数量关系;
(3)当四边形![]() 为正方形时,
为正方形时, ![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )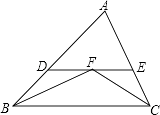
A.①②③
B.①②③④
C.①②
D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由. 
(3)拓展与应用:如图(3),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com