
【题目】如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=( )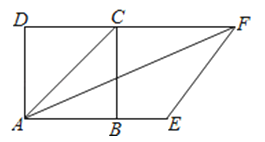
A.30°
B.45°
C.22.5°
D.135°
【答案】C
【解析】解:因为AC为正方形ABCD的对角线,则∠CAE=45°,又因为菱形的每一条对角线平分一组对角,则∠FAB=22.5°,
故选:C.
【考点精析】根据题目的已知条件,利用菱形的判定方法和正方形的性质的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了 ![]() (
( ![]() 为非负整数)的展开式的项数及各项系数的有关规律.
为非负整数)的展开式的项数及各项系数的有关规律.

(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过 ![]() 天是星期 .
天是星期 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.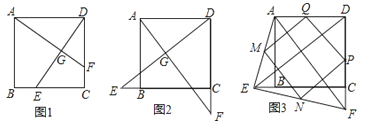
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=60',∠D=50°,将△CMN沿MN翻折得△EMN,若EM∥AB,EN∥AD,则∠C的度数为

A. 110° B. 115° C. 120° D. 125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合采用抽样调查的是( )
A. 某公司招聘人员,对应聘人员进行面试
B. 调查一批节能灯泡的使用寿命
C. 为保证火箭的成功发射,对其零部件进行检查
D. 对乘坐某次航班的乘客进行安全检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.

(1)求证:AE=CF.
(2)求证:四边形AFCE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com