
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.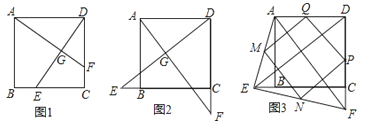
【答案】解:(1)上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,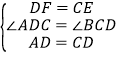 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥DE;
(2)上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,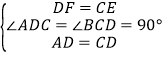 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠CDE=∠DAF,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥DE;
(3)四边形MNPQ是正方形.
理由为:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,
∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
∴MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,
AF,MQ∥DE,PQ∥AF,
∴四边形OHQG是平行四边形,
∵AF=DE,
∴MQ=PQ=PN=MN,
∴四边形MNPQ是菱形,
∵AF⊥DE,
∴∠AOD=90°,
∴∠HQG=∠AOD=90°,
∴四边形MNPQ是正方形.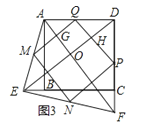
【解析】(1)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠DAF=∠CDE,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;
(2)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠E=∠F,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;
(3)首先设MQ,DE分别交AF于点G,O,PQ交DE于点H,由点M,N,P,Q分别为AE,EF,FD,AD的中点,即可得MQ=PN=![]() DE,PQ=MN=
DE,PQ=MN=![]() AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.


科目:初中数学 来源: 题型:
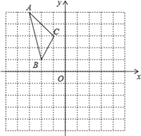
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 .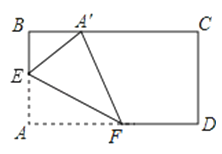
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了某种幼树在一定条件下移植成活情况
移植总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
成活的频率(精确到0.01) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
由此估计这种幼树在此条件下移植成活的概率约是_____(精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com