
【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 .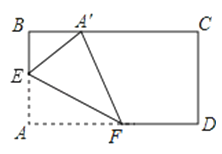
【答案】4cm≤A′C≤8cm
【解析】解: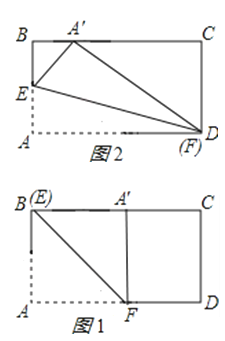
∵四边形ABCD是矩形,
∴∠C=90°,BC=AD=10cm,CD=AB=6cm,
当点E与B重合时,A′C最小,
如图1所示:
此时BA′=BA=6cm,
∴A′C=BC﹣BA′=10cm﹣6cm=4cm;
当F与D重合时,A′C最大,
如图2所示:
此时A′D=AD=10cm,
∴A′C= ![]() =8(cm);
=8(cm);
综上所述:A′C的取值范围为4cm≤A′C≤8cm.
所以答案是:4cm≤A′C≤8cm.
【考点精析】利用矩形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】(1)画线段AC=30mm(点A在左侧);
(2)以C为顶点,CA为一边,画∠ACM=90°;
(3)以A为顶点,AC为一边,在∠ACM的同侧画∠CAN=60°,AN与CM相交于点B;量得AB是多少mm?
(4)画出AB中点D,连接DC,此时量得DC是多少mm?请你猜想AB与DC的数量关系是:AB是DC的多少倍?
(5)作点D到直线BC的距离DE,且量得DE等于多少mm?请你猜想DE与AC的数量关系是:DE和AC的数量关系是?,位置关系是?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.

(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.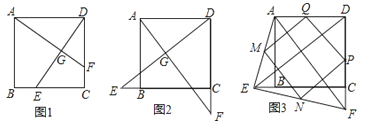
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3,则b、c的值为( )
A.b=2,c=2
B.b=2,c=0
C.b=﹣2,c=﹣1
D.b=﹣3,c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有60名学生,班长把全班学生对周末出游地的意向绘制成了扇形统计图,其中“想去重庆金佛山滑雪的学生数”的扇形圆心角是60°,则下列说法正确的是( )
A.想去重庆金佛山滑雪的学生有12人
B.想去重庆金佛山滑雪的学生肯定最多
C.想去重庆金佛山滑雪的学生占全班学生的 ![]()
D.想去重庆金佛山滑雪的学生占全班学生的60%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com