
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.

(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
【答案】(1)证明过程见解析;(2)DC=![]()
【解析】
试题分析:(1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;(2)首选得出△FOE≌△CBE(ASA),则BC=FO=![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
试题解析:(1)∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在![]() 的中点,∴
的中点,∴![]() =
=![]() ,
,
∴∠AOF=∠BOF, ∵∠ABC=∠ABG=90°, ∴∠AOF=∠ABG, ∴FO∥BG, ∵AO=BO,
∴FO是△ABG的中位线, ∴FO=![]() BG;
BG;
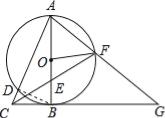
(2)在△FOE和△CBE中,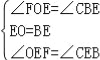 , ∴△FOE≌△CBE(ASA), ∴BC=FO=
, ∴△FOE≌△CBE(ASA), ∴BC=FO=![]() AB=2,
AB=2,
∴AC=![]() =2
=2![]() , 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
, 连接DB, ∵AB为⊙O直径, ∴∠ADB=90°, ∴∠ADB=∠ABC,
∵∠BCD=∠ACB, ∴△BCD∽△ACB, ∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得:DC=
, 解得:DC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2019年“五一”假期期间,我市共接待国内、外游客140.42万人次,实现旅游综合收入8.94亿元,则“旅游综合收入”用科学记数法表示正确的是( )
A. 1.4042×106B. 14.042×105C. 8.94×108D. 0.894×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 .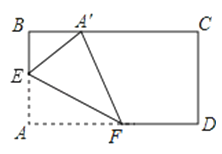
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华和李明周末去黄山鲁公园登山,张华每分钟登高10m,并且先出发30分钟,李明每分钟登高15m,两人同时登到山顶.
(1)设张华登山用了x分钟,请用含x的式子表示李明登山所用的时间;
(2)使用方程求出x的值;
(3)由x的值能求出山高吗?如果能,请求出山的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com