
【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积. 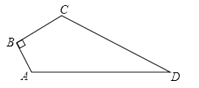
【答案】解:连接AC,如图所示: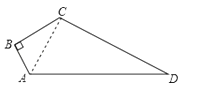
∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC=![]() =5,
=5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2 ,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×12=36.
×5×12=36.
故四边形ABCD的面积是36.
【解析】连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.


科目:初中数学 来源: 题型:
【题目】(1)画线段AC=30mm(点A在左侧);
(2)以C为顶点,CA为一边,画∠ACM=90°;
(3)以A为顶点,AC为一边,在∠ACM的同侧画∠CAN=60°,AN与CM相交于点B;量得AB是多少mm?
(4)画出AB中点D,连接DC,此时量得DC是多少mm?请你猜想AB与DC的数量关系是:AB是DC的多少倍?
(5)作点D到直线BC的距离DE,且量得DE等于多少mm?请你猜想DE与AC的数量关系是:DE和AC的数量关系是?,位置关系是?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A. 115° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了 ![]() (
( ![]() 为非负整数)的展开式的项数及各项系数的有关规律.
为非负整数)的展开式的项数及各项系数的有关规律.

(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过 ![]() 天是星期 .
天是星期 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在弧AB的中点,连接AF并延长与CB的延长线相交于点G,连接OF.

(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.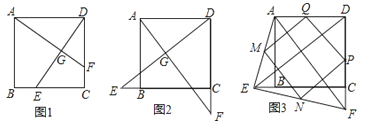
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3,则b、c的值为( )
A.b=2,c=2
B.b=2,c=0
C.b=﹣2,c=﹣1
D.b=﹣3,c=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com