
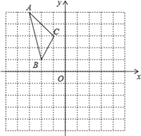
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
【答案】(1)点A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);



科目:初中数学 来源: 题型:
【题目】观察下列一组式的变形过程,然后回答问题: 例1: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ﹣1.
﹣1.
例2: ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]()
利用以上结论解答以下问题:
(1)![]() =;
=; ![]() =;
=;
(2)你用含n(n为正整数)的关系式表示上述各式子的变形规律.
(3)应用上面的结论,求下列式子的值. ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
(4)拓展提高,求下列式子的值. ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)画线段AC=30mm(点A在左侧);
(2)以C为顶点,CA为一边,画∠ACM=90°;
(3)以A为顶点,AC为一边,在∠ACM的同侧画∠CAN=60°,AN与CM相交于点B;量得AB是多少mm?
(4)画出AB中点D,连接DC,此时量得DC是多少mm?请你猜想AB与DC的数量关系是:AB是DC的多少倍?
(5)作点D到直线BC的距离DE,且量得DE等于多少mm?请你猜想DE与AC的数量关系是:DE和AC的数量关系是?,位置关系是?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A. 115° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.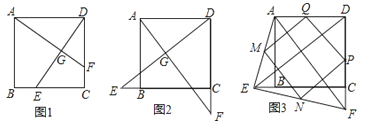
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com