
【题目】问题背景:如图1设P是等边△ABC内一点,PA=6,PB=8,PC=10,求∠APB的度数.小君研究这个问题的思路是:将△ACP绕点A逆时针旋转60°得到△ABP',易证:△APP'是等边三角形,△PBP'是直角三角形,所以∠APB=∠APP'+∠BPP'=150°.

简单应用:(1)如图2,在等腰直角△ABC中,∠ACB=90°.P为△ABC内一点,且PA=5,PB=3,PC=2![]() ,则∠BPC= °.
,则∠BPC= °.
(2)如图3,在等边△ABC中,P为△ABC内一点,且PA=5,PB=12,∠APB=150°,则PC= .
拓展廷伸:(3)如图4,∠ABC=∠ADC=90°,AB=BC.求证:![]() BD=AD+DC.
BD=AD+DC.
(4)若图4中的等腰直角△ABC与Rt△ADC在同侧如图5,若AD=2,DC=4,请直接写出BD的长.

【答案】(1)135;(2)13;(3)见解析;(4)![]()
【解析】
简单应用:(1)先利用旋转得出BP'=AP=5,∠PCP'=90°,CP'=CP=2![]() ,再根据勾股定理得出PP'=
,再根据勾股定理得出PP'=![]() CP=4,最后用勾股定理的逆定理得出△BPP'是以BP'为斜边的直角三角形,即可得出结论;
CP=4,最后用勾股定理的逆定理得出△BPP'是以BP'为斜边的直角三角形,即可得出结论;
(2)同(1)的方法得出∠APP'=60°,进而得出∠BPP'=∠APB﹣∠APP'=90°,最后用勾股定理即可得出结论;
拓展廷伸:(3)先利用旋转得出BD'=BD,CD'=AD,∠BCD'=∠BAD,再判断出点D'在DC的延长线上,最后用勾股定理即可得出结论;
(4)先利用旋转得出BD'=BD,CD=AD',∠DBD'=90°,∠BCD=∠BAD',再判断出点D'在AD的延长线上,最后用勾股定理即可得出结论.
解:简单应用:(1)如图2,
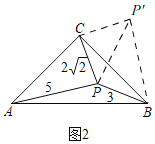
∵△ABC是等腰直角三角形,
∴∠ACB=90°,AC=BC,将
△ACP绕点C逆时针旋转90°得到△CBP',连接PP',
∴BP'=AP=5,∠PCP'=90°,CP'=CP=2![]() ,
,
∴∠CPP'=∠CP'P=45°,
根据勾股定理得,PP'=![]() CP=4,
CP=4,
∵BP'=5,BP=3,∴PP'2+BP2=BP',
∴△BPP'是以BP'为斜边的直角三角形,
∴∠BPP'=90°,
∴∠BPC=∠BPP'+∠CPP'=135°,
故答案为:135;
(2)如图3,

∵△ABC是等边三角形,
∴∠BAC=60°,AC=AB,
将△ACP绕点A逆时针旋转60°得到△ABP',连接PP',
∴BP'=CP,AP'=AP=5,∠PAP'=60°,
∴△APP'是等边三角形,
∴PP'=AP=5,∠APP'=60°,
∵∠APB=150°,
∴∠BPP'=∠APB﹣∠APP'=90°,
根据勾股定理得,BP'=![]() =13,
=13,
∴CP=13,
故答案为:13;
拓展廷伸:(3)如图4,
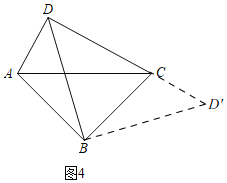
在△ABC中,∠ABC=90°,AB=BC,
将△ABD绕点B顺时针旋转90°得到△BCD',
∴BD'=BD,CD'=AD,∠BCD'=∠BAD,
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠BCD+∠BCD'=180°,
∴点D'在DC的延长线上,
∴DD'=CD+CD'=CD+AD,
在Rt△DBD'中,DD'=![]() BD,
BD,
∴![]() BD=CD+AD;
BD=CD+AD;
(4)如图5,

在△ABC中,∠ABC=90°,AB=BC,
连接BD,将△CBD绕点B顺时针旋转90°得到△ABD',
∴BD'=BD,CD=AD',∠DBD'=90°,∠BCD=∠BAD',
AB与CD的交点记作G,
∵∠ADC=∠ABC=90°,
∴∠DAB+∠AGD=∠BCD+∠BGC=180°,
∵∠AGD=∠BGC,
∴∠BAD=∠BCD,
∴∠BAD=∠BAD',
∴点D'在AD的延长线上,
∴DD'=AD'﹣AD=CD﹣AD=2,
在Rt△BDD'中,BD=![]() DD'=
DD'=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
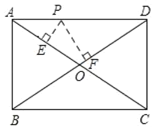
A.6B.12C.24D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
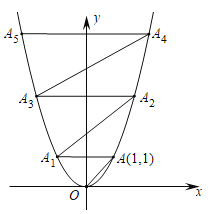
【题目】在平面直角坐标系中, 抛物线![]() 如图所示.已知
如图所示.已知![]() 点的坐标为
点的坐标为![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,过点
点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() …若依次进行下去,则点
…若依次进行下去,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c的对称轴为直线x=2,且顶点在x轴上.
(1)求b、c的值;
(2)画出抛物线的简图并写出它与y轴的交点C的坐标;
(3)根据图象直接写出:点C关于直线x=2对称点D的坐标 ;若E(m,n)为抛物线上一点,则点E关于直线x=2对称点的坐标为 (用含m、n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() (
(![]() 为常数.且
为常数.且![]() )的图象经过点
)的图象经过点![]() .
.![]() .
.
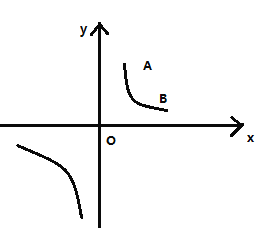
(1)求反比例函数的解析式及![]() 点的坐标;
点的坐标;
(2)在![]() 轴上找一点
轴上找一点![]() .使
.使![]() 的值最小,
的值最小,
①求满足条件的点![]() 的坐标;②求
的坐标;②求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 的面积为42.
的面积为42.
(1)如图,若点![]() 分别是边
分别是边![]() 的中点,则四边形
的中点,则四边形![]() 的面积是__________.
的面积是__________.

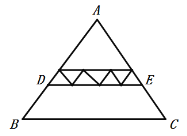
(2)如图,若图中所有的三角形均相似,其中最小的三角形面积为1,则四边形![]() 的面积是___________.
的面积是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com