
�龰�۲죺������ABCDֽƬ�ضԽ���AC�������õ���ABC�͡�A��C��D����ͼ1��ʾ��������A��C��D�Ķ���A�����A�غϣ����Ƶ�A����ʱ�뷽����ת��ʹ��D��A��A�䣩��B��ͬһ��ֱ���ϣ���ͼ2��ʾ��

�۲�ͼ2��֪����BC��ȵ��߶�������������������CAC��=�������������㣻
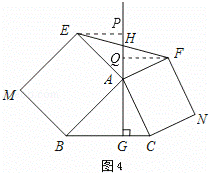
����̽������ͼ3����ABC�У�AG��BC�ڵ�G����AΪֱ�Ƕ��㣬�ֱ���AB��ACΪֱ�DZߣ����ABC��������Rt��ABE�͵���Rt��ACF������E��F������GA�Ĵ��ߣ�����ֱ�ΪP��Q����̽��EP��FQ֮���������ϵ����֤����Ľ��ۣ�
��չ���죺��ͼ4����ABC�У�AG��BC�ڵ�G���ֱ���AB��ACΪһ�����ABC��������ABME�;���ACNF������GA��EF�ڵ�H����AB=kAE��AC=kAF��̽��HE��HF֮���������ϵ����˵�����ɣ�
�⣺�۲�ͼ2���ɷ��֡�ABC�ա�AC��D����BC=AD����C��AD=��ACB��
���CAC��=180��﹣��C��AD﹣��CAB=90�㣻
�ʴ�Ϊ��AD��90��
����̽����FQ=EP��
�������£�
�ߡ�FAQ+��CAG=90�㣬��FAQ+��AFQ=90�㣬
���AFQ=��CAG��ͬ����ACG=��FAQ��
�֡�AF=AC��
�ڡ�AFQ���CAG�У�
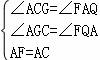 ��
��
���AFQ�ա�CAG��AAS����
��FQ=AG��
ͬ��EP=AG��
��FQ=EP��
��չ���죺HE=HF��
���ɣ�����E��EP��GA��FQ��GA������ֱ�ΪP��Q��
���ı���ABME�Ǿ��Σ�
���BAE=90�㣬
���BAG+��EAP=90�㣬
��AG��BC��
���BAG+��ABG=90�㣬
���ABG=��EAP��
�ߡ�AGB=��EPA=90�㣬
���ABG�ס�EAP��
��AG��EP=AB��EA��
ͬ����ACG�ס�FAQ��
��AG��FQ=AC��FA��
��AB=k•AE��AC=k•AF��
��AB��EA=AC��FA=k��
��AG��EP=AG��FQ��
��EP=FQ��
�֡ߡ�EHP=��FHQ����EPH=��FQH��
��Rt��EPH��Rt��FQH��
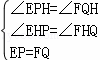 ��
��
��Rt��EPH��Rt��FQH��AAS����
��HE=HF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪һ������ֽƬOACB������ֽƬ������ƽ��ֱ������ϵ�У���A��11��0������B��0��6������PΪBC���ϵĶ��㣨��P�����B��C�غϣ���������O��P�۵���ֽƬ���õ�B����ۺ�OP����BP=t��
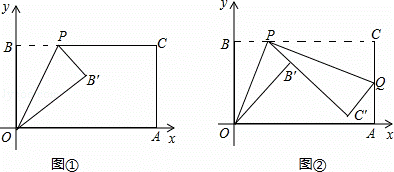
������ͼ�٣�����BOP=30��ʱ�����P�����ꣻ
������ͼ�ڣ�������P�ٴ��۵�ֽƬ��ʹ��C����ֱ��PB���ϣ��õ�C����ۺ�PQ����AQ=m�����ú���t��ʽ�ӱ�ʾm��
�����ڣ��������£�����C��ǡ�����ڱ�OA��ʱ�����P�����ֱ꣨��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
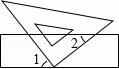
��ͼ��һ��ֱ�����ǰ��ֱ�Ƕ�������ֱ���ϣ�����1=56�㣬���2�Ķ���Ϊ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������ij����Ϊ�˸��õؿ�չ����������һСʱ�����Χ���š�����ϲ�����������Ŀ��ʲô��ֻдһ����������⣬��ȫУѧ������������������飬�����Ǹ��ݵõ���������ݻ��Ƶ�ͳ��ͼ��һ���֣�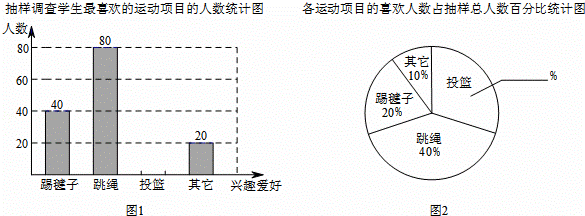
���꼶����ͳ�Ʊ�
�꼶 ���꼶 ���꼶 ���꼶
ѧ������ 850 680
�����������Ϣ����������⣺
��1����У�Զ�����ѧ�������˳������飿
��2���뽫ͼ1��ͼ2����������
��3����֪��У���꼶ѧ���Ⱦ��꼶ѧ����20�ˣ����㲹ȫ�ϱ����������������ݹ���ȫУѧ������ϲ�������˶�������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
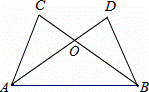
��ͼ����֪BD=AC����ô����һ�������������ܵõ���ABC�ա�BAD��ֻ��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����������ȷ���ǣ�������
�� A�� a0=1 B�� 3a•4a=12a C�� a12��a3=a4 D�� ��a3��4=a12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
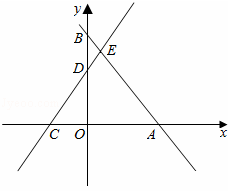
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᡢy��ֱ��ڵ�A��B��ֱ��CD��x�ᡢy��ֱ��ڵ�C��D��AB��CD�ཻ�ڵ�E���߶�OA��OC�ij���һԪ���η���x2﹣18x+72=0��������OA��OC����BE=5��tan��ABO=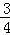 ��
��
��1�����A��C�����ꣻ
��2��������������y=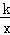 ��ͼ����E����k��ֵ��
��ͼ����E����k��ֵ��
��3������P���������ϣ���ƽ�����Ƿ����һ��Q��ʹ�Ե�C��E��P��QΪ������ı����Ǿ��Σ������ڣ���д�����������ĵ�Q�ĸ�������ֱ��д��λ��x���·��ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com