
����Ŀ����֪���ڡ�ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����������ADEF������CF��
��1����ͼ1������D���߶�BC��ʱ����֤��BD��CF��BD=CF��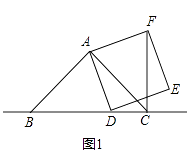
��2����ͼ2������D���߶�BC���ӳ�����ʱ�������������䣬�ڣ�1���ʽ��ۻ������𣿲�˵�����ɣ�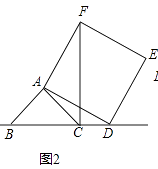
��3����ͼ3������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣺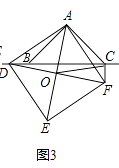
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
�������������ζԽ���AE��DF������ΪO������OC��̽����AOC����״����˵�����ɣ�
���𰸡�
��1��
֤�����ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAC=��BAD+��DAC=90�㣬��DAF=��CAF+��DAC=90�㣬
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У� 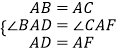
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45�㣬
���ACF+��ACB=90�㣬
��BD��CF��
��2��
��1���Ľ�����Ȼ���������ɣ�
�ߡ�BAD=��BAC+��CAD=90��+��CAD��
��CAF=��DAF+��CAD=90��+��CAD��
���BAD=��CAD��
�ڡ�BAD�͡�CAF�У� 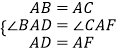
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45��
���BCF=��ACB+��ACF=45��+45��=90��
��BD��CF��
��3��
��BC��CD��CF�Ĺ�ϵ��CD=BC+CF
���ɣ��루1��ͬ����֤��BAD�ա�CAF���Ӷ��ɵã�
BD=CF��
����CD=BC+CF
�ڡ�AOC�ǵ���������
���ɣ��루1��ͬ����֤��BAD�ա�CAF���ɵã���DBA=��FCA��
�֡ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ABD=180�㩁45��=135�㣬
���ABD=��FCA=135��
���DCF=135�㩁45��=90��
���FCDΪֱ�������Σ�
�֡��ı���ADEF�������Σ��Խ���AE��DF�ཻ�ڵ�O��
��OC= ![]() DF��
DF��
��OC=OA
���AOC�ǵ���������
����������1���跨֤����BAD�ա�CAF���FCD=90�㼴�ɣ���2���루1��ͬ������3���еĢ��루1����ͬ����֤��BD=CF���ֵ�D��B��C���ߣ��ʣ�CD=BC+CF�����ɣ�1�����벢֤��BD��CF���Ӷ���֪��FCDΪֱ�������Σ����������εĶԽ��ߵ������ж���AOC���ߵ��ص㣬�ٽ�һ���ж�����״��
�����㾫����������Ҫ�����˵��������ε����ʵ����֪ʶ�㣬��Ҫ���յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ�������ȷ�����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m+n=7��mn=12����m2+n2��ֵ�ǣ�������
A. 1 B. 25 C. 2 D. ��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�ķ����˶�����1�δ�ԭ���˶�����1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�����������������˶����ɣ�����2017���˶�����P������Ϊ �� 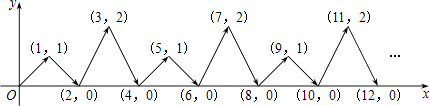
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�麬45��ǵ����ǰ��ֱ�Ƕ��㿿�ڳ��ߣ�����a��b����һ��b�ϣ�����1=30�㣬�����ǰ��б���볤�ߵ���һ��a�ļнǡ�2�Ķ���Ϊ�� �� 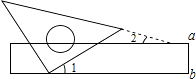
A.10��
B.15��
C.30��
D.35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ABCDE�У���A+��B+��E=����DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ� �� 
A.![]() ����90��
����90��
B.90�� ![]()
C.![]()
D.540�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷ���x2+6x+2=0�䷽��(x+p)2+q=0����ʽ��p2+q2��ֵ�ǣ� ��
A. 64B. 58C. 40D. 37
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���(a-2)x2+x+a2-4=0��һ������0,��a��ֵΪ�� ��
A. 2B. -2C. 2��-2D. 0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com