
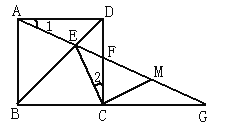
����Ŀ����ͼ��������ABCD�У�E��BD��һ�㣬AE���ӳ��߽�CD��F����BC���ӳ�����G��M��FG���е�.
��1����֤���� ��1=��2���� EC��MC.
��2�����ʵ���1���ڶ��ٶ�ʱ����ECGΪ���������Σ���˵������.
���𰸡���1����֤������������֤������������2������1=30��ʱ����ECGΪ����������. ���ɼ�����.
�������������������1���ٸ��������εĶԽ���ƽ��һ��Խǿɵ�![]() Ȼ�����ñ߽DZ߶���֤��
Ȼ�����ñ߽DZ߶���֤��![]() ��
��![]() �ٸ���ȫ�������ζ�Ӧ����ȼ���֤����
�ٸ���ȫ�������ζ�Ӧ����ȼ���֤����
�ڸ�����ֱ��ƽ�У��ڴ�����ȿɵ�![]() �ٸ���ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�
�ٸ���ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�![]() Ȼ��ݵȱ߶ԵȽǵ����ʵõ�
Ȼ��ݵȱ߶ԵȽǵ����ʵõ�![]() ������
������![]() Ȼ�����
Ȼ�����![]() ����֤��
����֤��![]() �Ӷ���֤��
�Ӷ���֤��
��2�����ݣ�1���Ľ��ۣ���ϵ����������������![]() Ȼ�����������ε��ڽǺͶ�����ʽ���м��㼴����⣮
Ȼ�����������ε��ڽǺͶ�����ʽ���м��㼴����⣮
���������(1)֤�����١��ı���ABCD�������Σ�
���ADE=��CDE��AD=CD��
�ڡ�ADE���CDE,
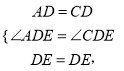
���ADE�ա�CDE(SAS)��
���1=��2��
�ڡ�AD��BG(�����εĶԱ�ƽ��)��
���1=��G��
��M��FG���е㣬
��MC=MG=MF��
���G=��MCG��
�֡ߡ�1=��2��
���2=��MCG��
��![]()
��![]()
��EC��MC��
��2������1=30��ʱ�� ![]() Ϊ����������. �������£�
Ϊ����������. �������£�
��![]() Ҫʹ
Ҫʹ![]() Ϊ���������Σ�����
��������������![]()
��![]()
��![]()
��![]()
��![]()
���1=30��.
�����͡������
��������
24
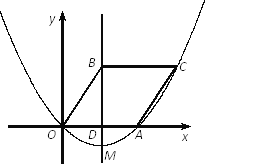
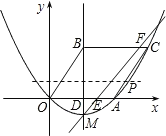
����Ŀ����ͼ����֪�����߾���ԭ��O�͵�A����B(2,3)�Ǹ������߶Գ�����һ�㣬����B��BC��x�ύ�������ڵ�C������BO��CA�����ı���OACB��ƽ���ı���.
��1���� ֱ��д��A��C��������ꣻ�� �����������ߵĺ�����ϵʽ��
��2����������ߵĶ���ΪM�������߶�AC���ҳ������ĵ�P��ʹ����PBM����BMΪ�ױߵĵ��������β������ʱ��P�����ꣻ
��3��������M��ֱ�߰��� OACB�������Ϊ1:3�����֣�������ֱ�ߵĺ�����ϵʽ.
���𰸡���1���� A(4,0)��C(6,3) ��������������ߺ�����ϵʽΪ![]() ����2����P������Ϊ(
����2����P������Ϊ(![]() ,1).
,1).
��3������ֱ��Ϊ��x=2��y=![]() x
x![]()
�������������������1���ٸ��ݵ�B(2,3)�Ǹ������߶Գ�����һ�㣬�ó�A������Ϊ(4,0)�������ó�AO�ij������ɵó�BC=AO�����C�����꼴�ɣ�
�ڸ���![]() �������꣬���ô���ϵ����������κ����Ľ���ʽ���ɣ�
�������꣬���ô���ϵ����������κ����Ľ���ʽ���ɣ�
��2���������![]() ���ڽ���ʽ�������ó����������ĵ�����PBM���ǵĶ���P���߶�BM�Ĵ�ֱƽ�������߶�AC�Ľ����ϣ�������ɣ�
���ڽ���ʽ�������ó����������ĵ�����PBM���ǵĶ���P���߶�BM�Ĵ�ֱƽ�������߶�AC�Ľ����ϣ�������ɣ�
��3����������֪������M�Ұ�OACB�������Ϊ1:3�����ֵ�ֱ�����������ֱ�ó����ɣ�
���������(1)�١ߵ�B(2,3)�Ǹ������߶Գ�����һ�㣬
��A������Ϊ(4,0)��
���ı���OACB��ƽ���ı��Σ�
��BC=AO��
��C��������(6,3)��
���������������Ϊ![]() �������⣬��
�������⣬��
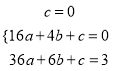 ,
,
��ã� 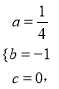
������������ߺ�����ϵʽΪ�� ![]()
(2)���߶�AC���ڵ�ֱ�ߵĺ�����ϵʽΪ![]() �������⣬��
�������⣬��
![]() ��ã�
��ã� 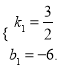
��ֱ��AC�ĺ�����ϵʽΪ�� ![]()
��![]()
�������ߵĶ�������MΪ(2,1)��
����������ĵ�����PBM���ǵĶ���P���߶�BM�Ĵ�ֱƽ�������߶�AC�Ľ����ϣ�
��BM=4,����P���������Ϊ1,��y=1����![]() ��,��
��,��![]()
���P������Ϊ![]()
(3)ƽ���ı��ε����ĶԳ��Կ��Եõ�������M�Ұ�![]() �������Ϊ1:3�����ֵ�ֱ��������,
�������Ϊ1:3�����ֵ�ֱ��������,
(��)��OACB=OABD=4��3=12,��OBD�����![]()
��ֱ��x=2Ϊ����,
(��)�������������һֱ�߷ֱ���x�ᡢBC���ڵ�![]()
��![]()
���ı���ACFE�����![]()
��![]()
��BC��x�ᣬ
���MDE�ס�MBF��
��![]()
��![]()
��![]()
��![]()
��![]()
��ֱ��ME�ĺ�����ϵʽΪ![]() ��
��
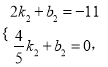
��ã� 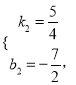
��ֱ��ME�ĺ�����ϵʽΪ![]()
�ۺ�(��)(��)��,����ֱ��Ϊ��x=2��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ҵ�ס�����ͽṹͼ�����ݽṹͼ�ṩ����Ϣ������������⣺
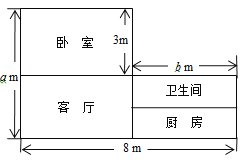
��1���ú�a��b�Ĵ���ʽ��ʾС���ҵ�ס�������S��
��2��С���������������������ש�����������õĵ�ש�۸�Ϊÿƽ����50Ԫ�������䡢�����Ϳ������õĵ�ש�۸�Ϊÿƽ����40Ԫ�����ú�a��b�Ĵ���ʽ��ʾ�����ש���ܷ���W��
��3���ڣ�2���������£���a��6��b��4ʱ����W��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
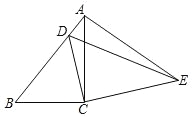
����Ŀ����ͼ������ABC�У���ACB=90����AB=9��cosB=![]() ������ABC���ŵ�C��ת��ʹ��B��AB���ϵĵ�D�غϣ���A���ڵ�E�����A��E֮��ľ���Ϊ ��
������ABC���ŵ�C��ת��ʹ��B��AB���ϵĵ�D�غϣ���A���ڵ�E�����A��E֮��ľ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ���������Լ��ˮ�����÷ֶμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������30������ʱ����2Ԫ/�����Ʒѣ�����ˮ������30������ʱ�����е�30��������2Ԫ/�������շѣ��������ְ�2.5Ԫ/�����Ʒѣ���ÿ����ͥ����ˮ��Ϊx�����ף�
��1����x������30ʱ��Ӧ�ն���ˮ�ѣ���x�Ĵ���ʽ��ʾ������x����30ʱ��Ӧ�ն���ˮ�ѣ���x�Ĵ���ʽ��ʾ����
��2��С�������·���ˮ20�����ף����·���ˮ36�����ף����С������һ��������������һ��Ӧ������Ԫˮ�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ����һ��¥CD�ĸ߶ȣ��ڵ�����A����¥CD�Ķ���C������Ϊ30������¥ǰ��50m����B�㣬�ֲ�õ�C������Ϊ60��. ���ⴱ¥CD�ĸ߶ȣ�����������ţ�.
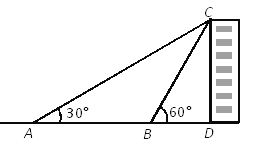
���𰸡��ô�¥CD�ĸ߶�Ϊ25![]() m .
m .
�������������������������ó�![]() �Ķ������������
�Ķ������������![]() ����������
����������![]() ������ɣ�
������ɣ�
��������������⣬��![]()
��![]()
��![]()
��![]()
��![]() ��
�� ![]() (m)��
(m)��
�� �ô�¥CD�ĸ߶�Ϊ25![]() m .
m .
�����͡������
��������
23
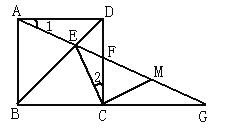
����Ŀ����ͼ��������ABCD�У�E��BD��һ�㣬AE���ӳ��߽�CD��F����BC���ӳ�����G��M��FG���е�.
��1����֤���� ��1=��2���� EC��MC.
��2�����ʵ���1���ڶ��ٶ�ʱ����ECGΪ���������Σ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD��BC����BAD=90�㣬CE��AD�ڵ�E��AD=8cm��BC=4cm��AB=5cm���ӳ�ʼʱ�̿�ʼ������P��Q �ֱ�ӵ�A��Bͬʱ�������˶��ٶȾ�Ϊ1cm/s������P��A��B����C����E�ķ����˶�������Eֹͣ������Q��B����C����E����D�ķ����˶�������Dֹͣ�����˶�ʱ��Ϊxs����PAQ�����Ϊycm2��������涨���߶������Ϊ0�������Σ�
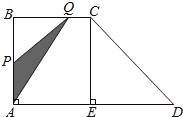
����������⣺
��1����x=2sʱ��y= cm2����x=![]() sʱ��y= cm2��
sʱ��y= cm2��
��2����5��x��14 ʱ����y��x֮��ĺ�����ϵʽ��
��3��������P���߶�BC���˶�ʱ�����![]() ʱx��ֵ��
ʱx��ֵ��
��4��ֱ��д���������˶������У�ʹPQ���ı���ABCE�ĶԽ���ƽ�е�����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Уѧ���ᷢ��ͬѧ�ǾͲ�ʱʣ��˽϶࣬�˷����أ���������У�ڳ����������ж�������ͬѧ����ϧ��ʳ��Ϊ����ͬѧ��������λ����Ҫ�ԣ�Уѧ������ij����ͺ���������˲���ͬѧ��ͷ��˵�ʣ��������������ͳ�ƺ���Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
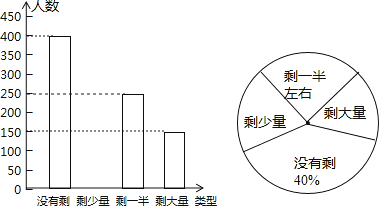
��1����α������ͬѧ���� ������ʣ������������Բ�Ľ��� ��
��2��������ͳ��ͼ����������
��3���ڱ������ѧ���������ȡһ��ǡ������ʣ����������ʣһ�����������ĸ��ʶ��
��4��Уѧ����ͨ�����ݷ�����������α����������ѧ��һ���˷ѵ�ʳ����Թ�200����һ�ͣ��ݴ˹��㣬��У18000��ѧ��һ���˷ѵ�ʳ��ɹ�������ʳ��һ�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����о���ѧ����ʱ����һ�����壺�������Ѿ��ź�˳�������![]() ��
��![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����������������Сֵ��Ϊ����
����������������Сֵ��Ϊ����![]() ��
��![]() ��
��![]() �����ֵ�����磬��������2��
�����ֵ�����磬��������2��![]() ��3����Ϊ
��3����Ϊ![]() ��
��![]() ��
��![]() ����������2��
����������2��![]() ��3�����ֵΪ
��3�����ֵΪ![]() ��
��
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�����ֵ��������![]() ��2��3�����ֵΪ
��2��3�����ֵΪ![]() ������3��
������3��![]() ��2�����ֵΪ1��
��2�����ֵΪ1��![]() �������о���С�����֣�������2��
�������о���С�����֣�������2��![]() ��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ
��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У����ֵ����СֵΪ![]() ���������ϲ��ϣ��ش��������⣺
���������ϲ��ϣ��ش��������⣺
��1��������![]() ��
��![]() ��2�����ֵ��
��2�����ֵ��
��2������![]() ��
��![]() ��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ�������� ��ȡ�����ֵ��Сֵ������Ϊ�������� ����д��һ�����ɣ���
��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���е����ֵ����СֵΪ�������� ��ȡ�����ֵ��Сֵ������Ϊ�������� ����д��һ�����ɣ���
��3����3��![]() ��
��![]() �����������ղ�ͬ��˳�����У��ɵõ����ɸ����У���ʹ���е����ֵΪ1����
�����������ղ�ͬ��˳�����У��ɵõ����ɸ����У���ʹ���е����ֵΪ1����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
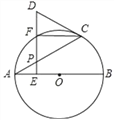
����Ŀ����ͼ��AB�ǡ�O��ֱ������P����AC��һ���㣨����A��C�غϣ�������P��PE��AB������ΪE������EP����AC�ڵ�F��������C�������ڵ�D��
��1����֤��DC��DP��
��2������CAB��30������F�ǻ�AC���е�ʱ���ж���A��O��C��FΪ������ı�����ʲô�����ı��Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com