
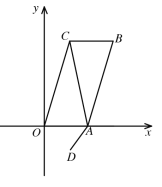
【题目】如图,在平面直角坐标系xOy中,O为原点,点A、C 的坐标分别为(2,0)、(1,3![]() ),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-
),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-![]() ).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
【答案】(-1,0)或(1,0)或(3,0)
【解析】
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论,根据平行四边形对角线互相平分,则两条对角线的中点相同,利用中点坐标公式建立方程求出a即可得到P点坐标.
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论:
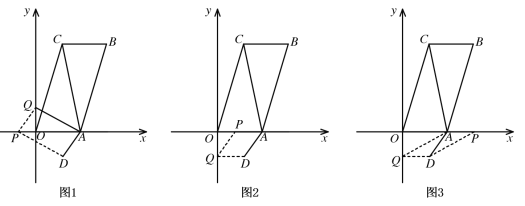
①如图1,当AP、DQ为对角线时,
∵A(2,0),D (1,-![]() ),由平行四边形对角线互相平分的性质和中点坐标公式可得,
),由平行四边形对角线互相平分的性质和中点坐标公式可得,
![]() ,解得
,解得![]() ,
,
∴P点坐标为(-1,0)
②如图2,当AQ、PD为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(1,0)
③如图3,当AD、PQ为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(3,0)
综上可得P点坐标为(-1,0)或(1,0)或(3,0)


科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
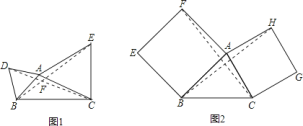
【题目】如图![]() ,以
,以![]() 边
边![]() 和
和![]() 为边作等边
为边作等边![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 判断
判断![]() 与
与![]() 的数量关系,并求
的数量关系,并求![]() 与
与![]() 的夹角
的夹角![]() 的度数;
的度数;
![]() 继续探索,如图
继续探索,如图![]() ,以
,以![]() 的
的![]() 和
和![]() 为边作正方形
为边作正方形![]() 和
和![]() ,连接
,连接![]() 、
、![]() ,判断
,判断![]() 和
和![]() 的数量关系,并求出此时
的数量关系,并求出此时![]() 与
与![]() 的夹角;
的夹角;
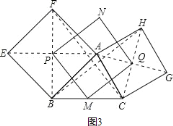
![]() 如图
如图![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接![]() ,判断四边形
,判断四边形![]() 的形状并证明.
的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() 的图象与性质,下列结论错误的是 ( )
的图象与性质,下列结论错误的是 ( )
A. 当x=3时,函数有最大值-2
B. 当x>3时,y随x的增大而减小
C. 抛物线可由 ![]() 经过平移得到
经过平移得到
D. 该函数的图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0;②b<c;③3a+c>0,其中正确结论两个数有______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程kx2-4x+2=0有实数根.
(1)求k的取值范围;
(2)若ABC中,AB=AC=2,AB、BC的长是方程kx2-4x+2=0的两根,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com