
【题目】已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:

(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由.
(4)粗略说一说易拉罐底面半径对所需铝质量的影响.
【答案】(1)易拉罐底面半径和用铝量的关系,易拉罐底面半径为自变量, 用铝量为因变量;(2)当底面半径为2.4cm时,易拉罐的用铝量为5.6cm3;(3)易拉罐底面半径为2.8cm时比较合适,因为此时用铝较少,成本低;(4)当易拉罐底面半径在1.6~2.8cm变化时,用铝量随半径的增大而减小,当易拉罐底面半径在2.8~4.0cm间变化时,用铝量随半径的增大而增大.
【解析】
(1)用铝量是随底面半径的变化而变化的,因而底面半径为自变量,用铝量为因变量;
(2)根据表格可以直接得到;
(3)选择用铝量最小的一个即可;
(4)根据表格,说明随底面半径的增大,用铝量的变化即可.
解:(1)易拉罐底面半径和用铝量的关系,易拉罐底面半径为自变量,用铝量为因变量;
(2)当底面半径为![]() 时,易拉罐的用铝量为
时,易拉罐的用铝量为![]()
(3)易拉罐底面半径为![]() 时比较合适,因为此时用铝较少,成本低
时比较合适,因为此时用铝较少,成本低
(4)当易拉罐底面半径在![]() 变化时,用铝量随半径的增大而减小,当易拉罐底面半径在
变化时,用铝量随半径的增大而减小,当易拉罐底面半径在![]() 间变化时,用铝量随半径的增大而增大.
间变化时,用铝量随半径的增大而增大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】体育课上的口令:立正,向右转,向后转,向左转之间可以相加.连结执行两个口令就把这两个口令加起来.例如:向右转+向左转=立正;向左转+向后转=向右转.如果分别用0,1,2,3分别代表立正,向右转,向后转,向左转,就可以用如图所示的加法表来表示,在表中填了部分的数值和代表数值的字母.下列对于字母![]() 的值,说法错误的是( )
的值,说法错误的是( )
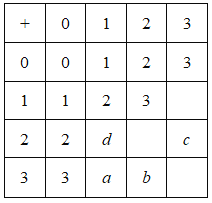
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
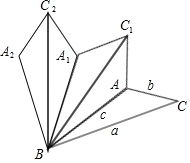
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水箱,它的容积为500L,水箱内原有水200L,现往水箱中注水,已知每分钟注水10L.
(1)写出水箱内水量![]() (L)与注水时间
(L)与注水时间![]() (min)的函数关系.
(min)的函数关系.
(2)求注水12min时水箱内的水量?
(3)需多长时间把水箱注满?
查看答案和解析>>
科目:初中数学 来源: 题型:
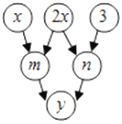
【题目】如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例: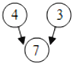 即
即![]()
则(1)用含![]() 的式子表示
的式子表示![]() ______;
______;
(2)当![]() 时,
时,![]() ______,
______,![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
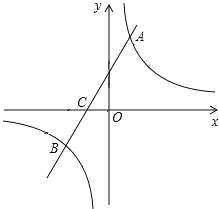
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
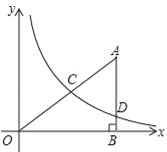
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
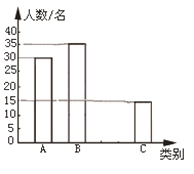
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com