【题目】如图，在菱形
中，
，
，点
是边
边的中点，点
、
分别是
、
上的两个动点，则
的最小值是________．
【答案】
【解析】
作DH⊥AC垂足为H与AG交于点E，点H关于AG的对称点为F，此时EF+ED最小=DH，先证明△ADC是等边三角形，在RT△DCH中利用勾股定理即可解决问题．
作DH⊥AC垂足为H与AG交于点E，
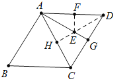
∵四边形ABCD是菱形，
∵AB=AD=CD=BC=6，
∵∠B=60°，
∴∠ADC=∠B=60°，
∴△ADC是等边三角形，
∵AG是中线，
∴∠GAD=∠GAC，
∴点H关于AG的对称点F在AD上，此时EF+ED最小=DH．
在RT△DHC中，∵∠DHC=90°，DC=6，∠CDH=
∠ADC=30°，
∴CH=DC=3，DH=
=
=3
，
∴EF+DE的最小值=DH=3，
故答案为：3．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】为响应团中央“号召全国每位团员，少先队员捐一瓶水”的倡议，我校师生积极开展了“情系西南灾区”的捐款活动．某班
名同学捐款的数额分别是（单位：元）：
，，，
，，
．则这组数据的中位数和众数分别是（ ）元．
A. 5，5 B. 10，5
C. 10，7.5 D. 7.5，5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：①AF=AC；②DF=CF；③∠AFC=∠C；④∠BFD=∠CAF．
其中正确的结论个数有． ( )
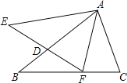
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图，航母由西向东航行，到达
处时，测得小岛
位于它的北偏东
方向，且与航母相距80海里，再航行一段时间后到达B处，测得小岛位于它的北偏东
方向.如果航母继续航行至小岛的正南方向的
处，求还需航行的距离
的长.
（参考数据：
，
，
，
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 y 与 x﹣2 成正比例，且当 x =﹣4 时， y =﹣3．
（1）求 y 与 x 的函数关系式；
（2）若点 M（5.1，m）、N（﹣3.9，n）在此函数图像上，判断 m 与 n 的大小关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．
（1）求证：DE是⊙O的切线；
（2）若AE=6，∠D=30°，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
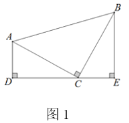
【题目】如图1 ,等腰直角三角形 ABC 中，∠ACB＝90°，CB＝CA，直线 DE 经过点 C，过 A 作 AD⊥DE 于点 D，过 B 作 BE⊥DE 于点 E，则△BEC≌△CDA，我们称这种全等模型为 “K 型全等”．（不需要证明）
（模型应用）若一次函数 y=kx+4（k≠0）的图像与 x 轴、y 轴分别交于 A、B 两点．
（1）如图 2，当 k=－1 时，若点 B 到经过原点的直线 l 的距离 BE 的长为 3，求点 A 到直线 l 的距离 AD 的长；
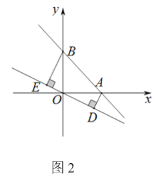
（2）如图 3，当 k=－ 
时，点 M 在第一象限内，若△ABM 是等腰直角三角形，求点
M 的坐标；
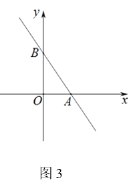
（3）当 k 的取值变化时，点 A 随之在 x 轴上运动，将线段 BA 绕点 B 逆时针旋转 90° 得到 BQ，连接 OQ，求 OQ 长的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用配方法解下列方程时，配方有错误的是（ ）
A．x2﹣2x﹣99=0化为（x﹣1）2=100
B．x2+8x+9=0化为（x+4）2=25
C．2t2﹣7t﹣4=0化为（t﹣
）2=
D．3x2﹣4x﹣2=0化为（x﹣
）2=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P为正方形ABCD的边CD上一点，BP的垂直平分线EF分别交BC、AD于E、F两点，GP⊥EP交AD于点G，连接BG交EF于点 H，下列结论：①BP=EF；②∠FHG=45°；③以BA为半径⊙B与GP相切；④若G为AD的中点，则DP=2CP．其中正确结论的序号是（ ）
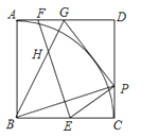
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com