
【题目】如图,![]() 的内接四边形
的内接四边形![]() 中
中![]() 为
为![]() 直径,
直径,![]() ,
,![]() 是
是![]() 的切线,
的切线,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
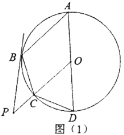
(1)如图(1)求证:![]() ;
;
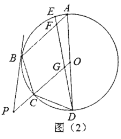
(2)如图(2)点![]() 在弧
在弧![]() 上,连接
上,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
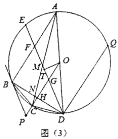
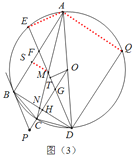
(3)如图(3)在(2)的条件下,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)DQ=14.
【解析】
(1)连接OB,根据切线性质∠CBP+∠OBC=90°,由OB=OC,结合三角形内角和易证∠BOC=2∠CBP,再由平行线性质可得∠BOC=∠ABO,∠COD=∠OAB,而∠OBA=∠OAB,所以∠COD=2∠CBP;
(2)由OC // AB可知∠AFE=∠DGC,将∠ADC+2∠.AFE=180°转化为∠OCD+2∠CGD=180°,即可得∠GCD=∠CDG,由等角对等边即可得到结论;
(3)连接AE、AQ,过M点作MS⊥AB于S,根据2∠ANB-∠ADQ=2∠ADB,可得四边形ABDQ为矩形,即DQ=AB,根据角的等量关系解三角形可知EF=![]() ,AE=
,AE=![]() ,设TM=|
,设TM=|![]() x,则DT=ET=4
x,则DT=ET=4![]() + x
+ x![]() ,DG=3
,DG=3![]() +
+ ![]() x,用三角函数可导出CD=CG=4+2x,GH=1+x, CD=3x+3,即4+2x=3x+3, 可得GH=4,BF=8,AF=6,即AB=DQ=14.
x,用三角函数可导出CD=CG=4+2x,GH=1+x, CD=3x+3,即4+2x=3x+3, 可得GH=4,BF=8,AF=6,即AB=DQ=14.
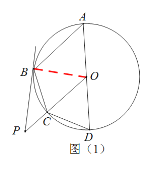
(1)连接OB,
∵BP是⊙O的切线,
∴OB⊥PB,
∵∠PBO=90,
∴∠CBP+∠OBC=90°,
∴2∠CBP+2∠OBC=180°,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠OBC+∠OCB+∠BOC=180°,
∴2∠OBC+∠BOC=180°,
∴∠BOC=2∠CBP,
∵OC∥AB,
∴∠BOC=∠ABO,∠COD=∠OAB,
∵OB=OA,
∴∠OBA=∠OAB,
∴∠COD=2∠CBP.
(2)∵OC∥AB,
∴∠AFE=∠OGF,
∵∠CGD=∠OGF,
∴∠AFE=∠DGC,
∵∠ADC+2∠AFE=180,
∵OD=OC∴∠GCD=∠ADC,
∴∠GCD+2∠AFE=180,
∵∠GCD+∠CDG+∠CGD=180°,
∴∠GCD=∠CDG,
∴CD=CG;

(3)连接AE、AQ,过M点作MS⊥AB于S.
∵AD为⊙O直径,
∴AE⊥DE,
∴∠AED=90,
∵OT⊥DE,
∴TE=TD,∠OTD=90,
∴OT=![]() ,
,
∵OC∥AB,
![]() ,
,
∵EF=2TG=2![]() ,
,
![]() ,
,
![]() ,
,
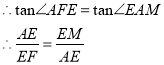
∵FM=![]() , 即EM=
, 即EM=![]() ,
,
∴AE=![]() ,
,
可得,tan∠EAF=![]() ,
,
解△AFM,可得tan∠FAM=![]() ,AF=6,
,AF=6,
设TM=![]() x,则
x,则![]()
用三角函数可导出CD=CG=![]() ,
,
∴CD=![]()
即![]()
解得![]()
∴GH=4,BF=8,AF=6
∴AB=14
∵∠ANB-∠ADB=∠CAD
又∵ 2∠ ANB-∠ADQ=2∠ADB,
∴∠ ADQ=2∠CAD,
由 (1) 可知∠BAD=2∠CAD,
∴∠ADQ= ∠BAD,
∴DQ∥AB∴四边形ABDQ的四角均为90°
∴四边形ABDQ为矩形,
∴DQ=AB=14


科目:初中数学 来源: 题型:
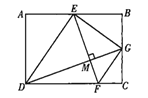
【题目】如图,点E是矩形ABCD的边AB的中点,点F是边CD上一点,连接ED,EF,ED平分∠AEF,过点D作DG⊥EF于点M,交BC于点G,连接GE,GF,若FG∥DE,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的300米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
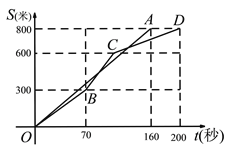
A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
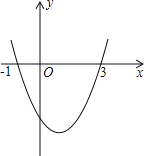
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
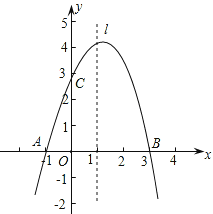
查看答案和解析>>
科目:初中数学 来源: 题型:
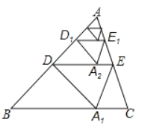
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,
处,称为第1次操作,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,
处,称为第2次操作,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去,经过第2019次操作后,
;按上述方法不断操作下去,经过第2019次操作后,![]() 到折痕
到折痕![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com