
【题目】为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
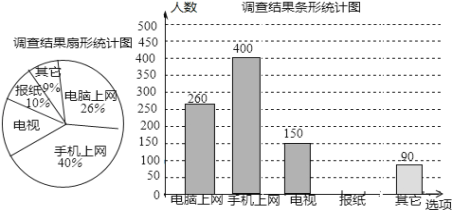
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是 ;请补全条形统计图;
(2)扇形统计图中,“电视”所对应的圆心角的度数是 ;
(3)若该市约有90万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数。
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足为D. 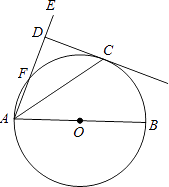
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半径;②求tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。
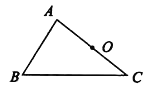
小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.
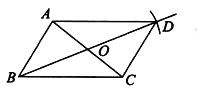
所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G. 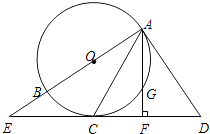
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1, 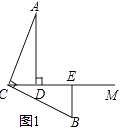
①线段CD和BE的数量关系是;
②请写出线段AD,BE,DE之间的数量关系 .
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系. 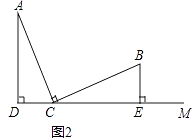
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中, ∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线. ①求证: ∠AFC=120°;②若AD=6,CE=4,求AC的长?
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
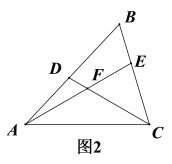
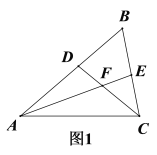
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com