
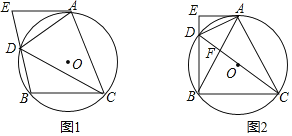
【题目】如图,四边形ADBC内接于⊙O,AD平分∠EDC,AE∥BC交直线BD于E.
(1)求证:AE是⊙O的切线;
(2)若CD为直径,tan∠ADE=2,求sin∠BDC的值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)连接AB,连接AO并延长交BC于F,由圆内接四边形的性质得出∠ADE=∠ACB,再由圆周角定理证出∠ABC=∠ACB,得出AB=AC,得出AF⊥BC,证出AE⊥AF即可得出结论;
(2)连接AO并延长交BC于G,由圆周角定理得出∠DAC=∠CBD=90°,证出四边形AEBG是矩形,得出BG=AE,AG=BE,由三角函数得出AE=2DE,AC=2AD,AG=2CG=BC=2AE=4DE,得出AD=![]() DE,CD=
DE,CD=![]() AD=5DE,即可得出结果.
AD=5DE,即可得出结果.
(1)证明:连接AB,连接AO并延长交BC于F,如图1所示:
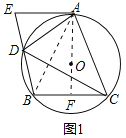
∵四边形ADBC内接于⊙O,AD平分∠EDC,
∴∠ADE=∠ACB,∠ADE=∠ADC,
∵∠ADC=∠ABC,
∴∠ABC=∠ACB,
∴AB=AC,
∴AF⊥BC
∵AE∥BC,
∴AE⊥AF,
∴AE是⊙O的切线;
(2)解:连接AO并延长交BC于G,如图2所示:
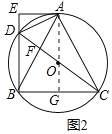
∵CD为直径,
∴∠DAC=∠CBD=90°,
∵AE∥BC,
∴∠E+∠CBD=90°,
∴∠E=90°,
∴四边形AEBG是矩形,
∴BG=AE,AG=BE,
∵∠ADE=∠ADC=∠ACB,
∴![]() ,
,
∴AE=2DE,AC=2AD,AG=2CG=BC=2AE=4DE,
∴AD=![]() DE,CD=
DE,CD=![]() AD=5DE,
AD=5DE,
∴![]() .
.


科目:初中数学 来源: 题型:
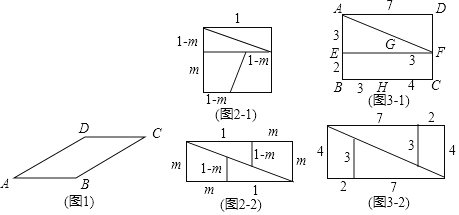
【题目】(1)如图1,在平行四边形ABCD中,∠A=30°,AB=6,AD=8,将平行四边形ABCD分割成两部分,然后拼成一个矩形,请画出拼成的矩形,并说明矩形的长和宽.(保留分割线的痕迹)
(2)若将一边长为1的正方形按如图2﹣1所示剪开,恰好能拼成如图2﹣2所示的矩形,则m的值是多少?
(3)四边形ABCD是一个长为7,宽为5的矩形(面积为35),若把它按如图3﹣1所示的方式剪开,分成四部分,重新拼成如图3﹣2所示的图形,得到一个长为9,宽为4的矩形(面积为36).问:重新拼成的图形的面积为什么会增加?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上学习越来越受到学生的喜爱.某校信息小组为了解七年级学生网上学习的情况,从该校七年级随机抽取20名学生,进行了每周网上学习的调查.数据如下(单位:时):
3 | 2.5 | 0.6 | 1.5 | 1 | 2 | 2 | 3.3 | 2.5 | 1.8 |
2.5 | 2.2 | 3.5 | 4 | 1.5 | 2.5 | 3.1 | 2.8 | 3.3 | 2.4 |
整理上面的数据,得到表格如下:
网上学习时间 |
|
|
|
|
人数 | 2 | 5 | 8 | 5 |
样本数据的平均数、中位数、众数如下表所示:
统计量 | 平均数 | 中位数 | 众数 |
数值 | 2.4 |
|
|
根据以上信息,解答下列问题:
(1)上表中的中位数![]() 的值为 ,众数
的值为 ,众数![]() 的值为 .
的值为 .
(2)用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间.
(3)已知该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 函数图象位于第一、三象限
B. 函数值y随x的增大而减小
C. 若A(-1,y1)、B(1,y2)、C(2,y3)是图象上三个点,则y1<y3<y2
D. P为图象上任意一点,过P作PQ⊥y轴于Q,则△OPQ的面积是定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题解决
糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?

反思归纳
现有![]() 根竹签,
根竹签,![]() 个山楂.若每根竹签串
个山楂.若每根竹签串![]() 个山楂,还剩余
个山楂,还剩余![]() 个山楂,则下列等式成立的是________(填写序号).
个山楂,则下列等式成立的是________(填写序号).
⑴![]() ;⑵
;⑵![]() ;⑶
;⑶![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
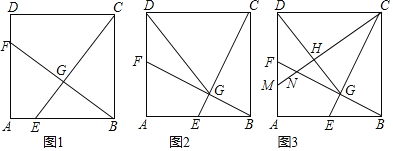
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,当点![]() 运动到
运动到![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,分别交
,分别交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
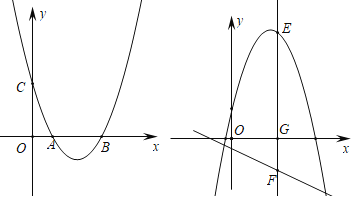
【题目】如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.
(1)求抛物线的表达式和顶点D的坐标;
(2)在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;
(3)将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=-![]() x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
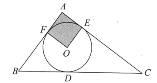
A.4B.6.25C.7.5D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com