
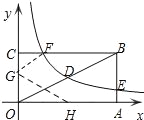
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.

(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
【答案】(1)2;(2)反比例函数解析式为y=![]() ,n=
,n=![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据点E的纵坐标判断出OA=4,再根据tan∠BOA=![]() 即可求出AB的长度;
即可求出AB的长度;
(2)根据(1)求出点B的坐标,再根据点D是OB的中点求出点D的坐标,然后利用待定系数法求函数解析式求出反比例函数解析式,再把点E的坐标代入进行计算即可求出n的值;
(3)先利用反比例函数解析式求出点F的坐标,从而得到CF的长度,连接FG,根据折叠的性质可得FG=OG,然后用OG表示出CG的长度,再利用勾股定理列式计算即可求出OG的长度.
试题解析:(1)∵点E(4,n)在边AB上,
∴OA=4,
在Rt△AOB中,∵tan∠BOA=![]() ,
,
∴AB=OA×tan∠BOA=4×![]() =2;
=2;
(2)根据(1),可得点B的坐标为(4,2),
∵点D为OB的中点,
∴点D(2,1)
∴![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y=![]() ,
,
又∵点E(4,n)在反比例函数图象上,
∴![]() =n,
=n,
解得n=![]() ;
;
(3)如图,设点F(a,2),
∵反比例函数的图象与矩形的边BC交于点F,
∴![]() =2,
=2,
解得a=1,
∴CF=1,
连接FG,设OG=t,则OG=FG=t,CG=2-t,
在Rt△CGF中,GF2=CF2+CG2,
即t2=(2-t)2+12,
解得t=![]() ,
,
∴OG=t=![]() .
.


科目:初中数学 来源: 题型:
【题目】一次普法知识竞赛共有30道题,规定答对一道题得4分,答错或不答,一道题得-1分,在这次竞赛中,小明获得优秀(90或90分以上),则小明至少答对了 道题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.

(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2(x﹣3)2+1,下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);
④当x<3时,y的值随x值的增大而减小.
则其中说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市体育中考项目分为必测项目和选测项目,必测项目为:跳绳、立定跳远;选测项目为50米、实心球、踢毽子三项中任选一项.
(1)每位考生将有 种选择方案;
(2)用画树状图或列表的方法求小颖和小华将选择同种方案的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=x2,下列说法不正确的是( )
A. 当x<0时,y随x增大而减小 B. 当x≠0时,函数值总是正的
C. 当x>0时,y随x增大而增大 D. 函数图象有最高点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月20日晚,中国首艘货运飞船天舟一号顺利发射升空。其在太空飞行速度是子弹飞行速度8倍,已知子弹的速度约为每秒300米,那么天舟一号的飞行速度用科学记数法(精确到千位)表示为( )厘米/秒.
A. 2.40×106 B. 2.4×105 C. 2.40×105 D. 2.4×103
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com