
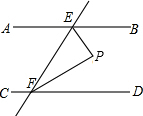
 已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.分析 (1)由邻补角的定义可求得∠BEF,再由角平分线的定义可求得∠PEF;
(2)由平行的性质可求得∠BEF+∠DFE=180°,再结合角平分线的定义可求得∠BEP+∠DFP=90°.
解答 解:(1)∵∠AEF+∠BEF=180°,
∴∠BEF=180°-∠AEF=180°-66°=104°,
又∵EP平分∠BEF,
∴∠PEF=$\frac{1}{2}$∠BEF=57°;
(2)∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EP平分∠BEF,FP平分∠DFE,
∴∠BEF=2∠BEP,∠DFE=2∠DFP,
∴∠BEP+∠DFP=90°.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同们角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
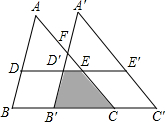 如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )
如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )| A. | ∠A=49° | B. | 四边形CC′E′E是平行四边形 | ||
| C. | B′C=DE | D. | S△ABC=5S△D′FE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
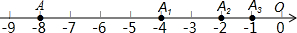 一条数轴如图所示,点A表示的数是-8.
一条数轴如图所示,点A表示的数是-8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1=y2>y3 | B. | y1=y3<y2 | C. | y1=y3=y2 | D. | y1>y2>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
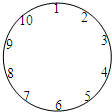 10个人围成一个圆圈做游戏,游戏的规则是:每人心里想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每人将与他相邻两个人的数据的平均数报出来,报出来的数如图所示,则报1的人心里想的数是6.
10个人围成一个圆圈做游戏,游戏的规则是:每人心里想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每人将与他相邻两个人的数据的平均数报出来,报出来的数如图所示,则报1的人心里想的数是6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com