
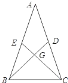
【题目】如图,在△ABC中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则tan∠ABC=________.
【答案】3
【解析】
连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,DE为△ABC的中位线,故BC=4x,四边形BCDE为等腰梯形,根据等腰梯形的性质可知,BF=![]() (BC-DE)=x,则FC=3x,又△BCG为等腰直角三角形,故△CEF为等腰直角三角形,则EF=CF=3x,解Rt△BEF可求解.
(BC-DE)=x,则FC=3x,又△BCG为等腰直角三角形,故△CEF为等腰直角三角形,则EF=CF=3x,解Rt△BEF可求解.
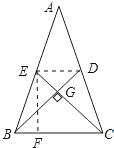
如图,连接DE,过E点作EF⊥BC,垂足为F,
设DE=2x,
依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=![]() (BCDE)=x,则FC=3x,
(BCDE)=x,则FC=3x,
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,
∴tan∠ABC=![]() =
=![]() =3.
=3.
故答案为:3.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
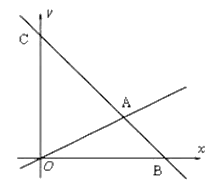
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与![]() 轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O
轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O![]() A
A![]() C运动.
C运动.
(1)求直线BC的解析式.
(2)求![]() 的面积.
的面积.
(3)当![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 时,求出这时点P的坐标.
时,求出这时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
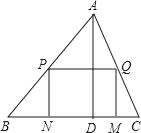
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
为了考察甲、乙两种成熟期小麦的株高长势状况,现从中各随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 | 63 | 66 | 63 | 61 | 64 | 61 |
乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交试验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况.请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.0.350是精确到0.001的近似数
B.3.80万是精确到百位的近似数
C.一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为51.0
D.近似数2.20是由数![]() 四舍五入得到的,那么数
四舍五入得到的,那么数![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座石拱桥的桥拱是以![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.
为半径的一段圆弧.

![]() 请你确定弧
请你确定弧![]() 的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
的中点;(要求:用尺规作图,保留作图痕迹,不写作法和证明)
![]() 如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为
如果已知石拱桥的桥拱的跨度(即弧所对的弦长)为![]() 米,拱高(即弧的中点到弦的距离)为
米,拱高(即弧的中点到弦的距离)为![]() 米,求桥拱所在圆的半径.
米,求桥拱所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴的两个交点A,B关于直线x=﹣1对称,且AB=6,顶点在函数y=2x的图象上,则这个二次函数的表达式为________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com