
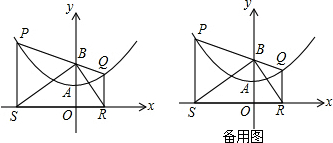
���� ��1����������ó���������꣬�������ߵĽ���ʽΪy=ax2+1���ѣ�2��2��������ݴ���ϵ�����Ϳ�����������ߵĽ���ʽ��
��2���ٹ���B��BN��PS������ΪN��������P�������ǣ�a��$\frac{1}{4}$a2+1�������ݹ��ɶ����Ϳ�����a��ʾ��PB=PS�ij���ͬ����֪BQ=QR�����ݵȱ߶ԵȽǾͿ���֤����SBR=90�ȣ����SBRΪֱ�������Σ�
������P��S��MΪ���������������Q��M��RΪ��������������ƣ��С�PSM�ס�MRQ�͡�PSM�ס�QRM����������������������εĶ�Ӧ�ߵı���ȾͿ��������
��3����E��m��$\frac{1}{4}$m2+1������������ó�F��-m+2��$\frac{1}{4}$��-m+2��2+1����Ȼ��������ε���λ�߶����ó�$\frac{1}{4}$m2+1+$\frac{1}{4}$��-m+2��2+1=6���ⷽ�����m��ֵ���ó�E�����꣬Ȼ�����ô���ϵ�����������ֱ�ߵĽ���ʽ��
���  �⣺��1���ߵ�x=0ʱyȡ����Сֵ1��
�⣺��1���ߵ�x=0ʱyȡ����Сֵ1��
�ඥ��Ϊ��0��1����
�������ߵĽ���ʽΪy=ax2+1��
�ѣ�2��2�������2=4a+1��
����������飬��a=$\frac{1}{4}$��
��������ߵĽ���ʽΪy=$\frac{1}{4}$x2+1��
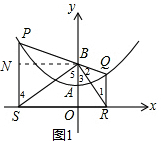
��2����֤������ͼ1������B��BN��PS������ΪN��
��P����������y=$\frac{1}{4}$x2+1�ϣ�����P������Ϊ��a��$\frac{1}{4}$a2+1����
��PS=$\frac{1}{4}$a2+1��OB=NS=2��BN=-a��
��PN=PS-NS=$\frac{1}{4}$a2-1��
��Rt��PNB��
PB2=PN2+BN2=��$\frac{1}{4}$a2-1��2+a2=��$\frac{1}{4}$a2+1��2
��PB=PS=$\frac{1}{4}$a2+1��
ͬ����֪BQ=QR��
���1=��2��
�֡ߡ�1=��3��
���2=��3��
ͬ����SBP=��5��
��2��5+2��3=180��
���5+��3=90��
���SBR=90�ȣ�
���SBRΪֱ�������Σ�
����ͼ2����QN��PS��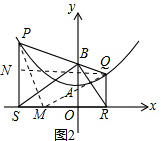
��PS=b��QR=c��
���ɢ�֪PS=PB=b��QR=QB=c��PQ=b+c��PN=b-c��
��QN2=SR2=��b+c��2-��b-c��2
��SR=2$\sqrt{bc}$��
������ڵ�M����MS=x����MR=2$\sqrt{bc}$-x��
��ʹ��PSM�ס�MRQ��
���� $\frac{b}{x}$=$\frac{2\sqrt{bc}-x}{c}$��
��x2-2$\sqrt{bc}$x+bc=0
��x1=x2=$\sqrt{bc}$��
��SR=2$\sqrt{bc}$��
��MΪSR���е㣮
��ʹ��PSM�ס�QRM��
����$\frac{b}{x}$=$\frac{c}{2\sqrt{bc}-x}$��
��x=$\frac{2b\sqrt{bc}}{b+c}$��
��$\frac{MR}{MS}$=$\frac{2\sqrt{bc}-x}{x}$=$\frac{2\sqrt{bc}}{\frac{2b\sqrt{bc}}{b+c}}$-1=$\frac{c}{b}$=$\frac{QB}{BP}$=$\frac{RO}{OS}$��
��M�㼴Ϊԭ��O��
��������������MΪSR���е�ʱ����PSM�ס�MRQ��
����MΪԭ��ʱ����PSM�ס�MRQ��
��3����ͼ3���ֱ��E��C��F��EG��x����G��CK��x����K��FH��x����H��
��E��m��$\frac{1}{4}$m2+1����
��C��ǡ�����߶�EF���е㣬C��1��3����
��GK=HK=-m+1��
��OH=-m+1+1=-m+2��
��F��-m+2��$\frac{1}{4}$��-m+2��2+1����
��CK=$\frac{1}{2}$��EG+FH��=3��
��$\frac{1}{4}$m2+1+$\frac{1}{4}$��-m+2��2+1=6��
�����ã�m2-2m-6=0��
���m=1��$\sqrt{7}$��
��E��1-$\sqrt{7}$��3-$\frac{\sqrt{7}}{2}$����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{3-\frac{\sqrt{7}}{2}=��1-\sqrt{7}��k+b}\\{3=k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$��
��ֱ��EF�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{5}{2}$��
���� ������Ҫ�����˴���ϵ������������ʽ�����������εĶ�Ӧ�ߵı�����Լ����ε���λ�߶�����


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
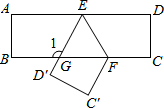 ��ͼ����һ�ų�����ֽƬABCD��EF�۵���ED����BC���ڵ�ΪG����D����C�ֱ����ڵ�D�䡢��C���λ���ϣ�����EFG=58�㣬���1=116�㣮
��ͼ����һ�ų�����ֽƬABCD��EF�۵���ED����BC���ڵ�ΪG����D����C�ֱ����ڵ�D�䡢��C���λ���ϣ�����EFG=58�㣬���1=116�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com