
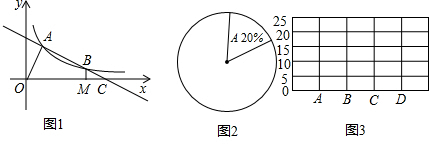
分析 (1)根据选A的人数及在扇形中所占的比例即可得出九年级一班的学生总数,设选答案C的人数为x,则选答案B的人数为(x-5)人,选答案D的人数为$\frac{1}{4}$x人,根据题意列出方程即可求得.
(2)用选各答案的人数除以总人数得出百分比,再画图即可解答.
(3)连结OB,设B点坐标为(a,b),将B点坐标代入反比例解析式得到ab=k,确定出OM与BM的长,根据OM=2MC,表示出MC长,进而表示出三角形BOM与三角形BMC的面积,两面积之和表示出三角形BOC的面积,由AB=BC,确定出三角形AOC的面积,由S△OAC=12列出关于k的方程,解方程即可求出k的值.
解答 解:(1)九年级一班学生总数=10÷20%=50人,
选答案B、C、D的总人数=50-10=40人,
设选答案C的人数为x,则选答案B的人数为(x-5)人,选答案D的人数为$\frac{1}{4}$x人,
根据题意得:x+x-5+$\frac{1}{4}$x=40,解得x=20,
x-5=15(人),$\frac{1}{4}$x=5(人)
答:选择答案B,C,D的人数分别为15、20、5人.
(2)如图所示: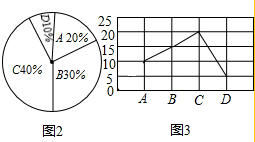
(3)B;
如图1,连结OB,
设B(a,b).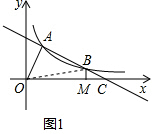 ∵点B在函数y=$\frac{k}{x}$上,
∵点B在函数y=$\frac{k}{x}$上,
∴ab=k,且OM=a,BM=b,
∵OM=2MC,
∴MC=$\frac{1}{2}$a,
∴S△BOM=$\frac{1}{2}$ab=$\frac{1}{2}$k,S△BMC=$\frac{1}{2}$×$\frac{1}{2}$ab=$\frac{1}{4}$ab=$\frac{1}{4}$k,
∴S△BOC=S△BOM+S△BMC=$\frac{1}{2}$k+$\frac{1}{4}$k=$\frac{3}{4}$k,
∵AB=BC,
∴S△AOB=S△BOC=$\frac{3}{4}$k,
∴S△AOC=S△AOB+S△BOC=$\frac{3}{2}$k,
∵S△AOC=12,
∴$\frac{3}{2}$k=12,
∴k=8.
故选B.
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数的性质是解本题的关键.也考查的是折线图和扇形统计图的综合运用.


科目:初中数学 来源: 题型:解答题
 小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题:
小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
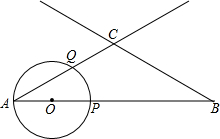 如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.
如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
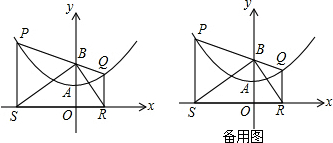
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com