
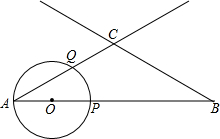
 ��ͼ��AB=3����A=��B=30�㣬����O��A��������AB������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��1.5������OΪԲ�ģ�OA��Ϊ�뾶�ġ�O������AB��AC����һ������ֱ�ΪP��Q������CP��PQ��
��ͼ��AB=3����A=��B=30�㣬����O��A��������AB������1����λ����/����ٶ������˶����˶�ʱ��Ϊt���룩��0��t��1.5������OΪԲ�ģ�OA��Ϊ�뾶�ġ�O������AB��AC����һ������ֱ�ΪP��Q������CP��PQ������ ��1���ȹ���C��CO��BC��AB�ڵ�O����ʱ��O��ֱ��BC���У�����AO=x������RT��OCB�г�������⼴�ɣ�
��2����ͼ�ɵ÷��������������0��t��$\frac{3}{4}$ʱ���߶�PC�͡�Oֻ��һ�����㣻�ڵ�1��t��1.5ʱ���߶�PC�͡�Oֻ��һ�����㣻
��3������������ٵ�t��1ʱ���ڵ�t=1ʱ����1��t��1.5ʱ�ֱ���⼴�ɣ�
��� �⣺��1����ͼ1������C��CO��BC��AB�ڵ�O��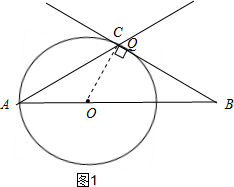
�ߡ�A=��B=30�㣬
���ACB=120�㣬
�֡ߡ�OCB=90�㣬
���OCA=30�㣬
���ʱ��O��ֱ��BC���У�
��AO=x����BO=3-x��
��AO=OC��
��RT��OCB��3-x=2x��
���x=1��
�൱t=1ʱ����O��ֱ��BC���У�
��2������ͼ2����CD��AB��AB�ڵ�D��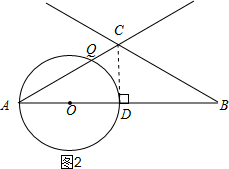
��AB=3����A=��B=30�㣬
��AD=$\frac{3}{2}$��
��AO=$\frac{3}{4}$��
�൱0��t��$\frac{3}{4}$ʱ���߶�PC�͡�Oֻ��һ�����㣻
�ڵ�1��t��1.5ʱ���߶�PC�͡�Oֻ��һ�����㣬
������������0��t��$\frac{3}{4}$��1��t��1.5ʱ���߶�PC�͡�Oֻ��һ�����㣻
��3���ٵ�t��1ʱ����ͼ3����CD��AB��AB�ڵ�D��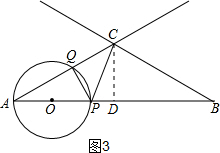
��AB=3����A=��B=30�㣬
��AD=$\frac{3}{2}$��
��AC=$\sqrt{3}$��
�ߡ�AQP=90�㣬��A=30�㣬
��AQ=$\frac{\sqrt{3}}{2}$AP=$\sqrt{3}$AO��QP=AO��
��QC=AC-AQ=$\sqrt{3}$-$\sqrt{3}$AO��
��S=$\frac{1}{2}$QC•QP=$\frac{1}{2}$��$\sqrt{3}$-$\sqrt{3}$t��•t=-$\frac{\sqrt{3}}{2}$��t-$\frac{1}{2}$��2+$\frac{\sqrt{3}}{8}$��
��S�����ֵΪ$\frac{\sqrt{3}}{8}$��
�ڵ�t=1ʱ��S=0��
��1��t��1.5ʱ����ͼ4��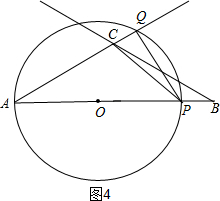
�ߡ�AQP=90�㣬��A=30�㣬
��AQ=$\frac{\sqrt{3}}{2}$AP=$\sqrt{3}$AO��QP=AO��
��AC=$\sqrt{3}$��
��QC=AQ-AC=$\sqrt{3}$AO-$\sqrt{3}$��
��S=$\frac{1}{2}$QC•QP=$\frac{1}{2}$��$\sqrt{3}$t-$\sqrt{3}$��•t=$\frac{\sqrt{3}}{2}$��t-$\frac{1}{2}$��2-$\frac{\sqrt{3}}{8}$��
�൱t=1.5ʱ��S�����ֵΪ$\frac{3\sqrt{3}}{8}$��
���� ������Ҫ������Բ���ۺ��⣬�漰���ߣ����������Σ�����ֱ�������μ������ε����������Ĺؼ��Ǹ��������ȷ��������⣬��Ҫ©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
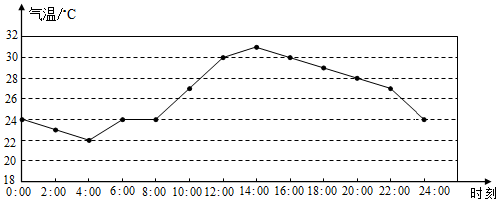
| A�� | ��һ������������30�� | B�� | ��һ��24��00�ﵽ������� | ||
| C�� | ������һ��7��00��������24�� | D�� | ������һ��15��00��������28�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com