
【题目】如图1,△ABC是等腰三角形,O是底边BC中点,腰AB与⊙O相切于点D
(1)求证:AC是⊙O的切线;
(2)如图2,连接CD,若tan∠BCD=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求BC的长.
,求BC的长.
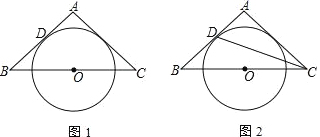
【答案】(1)证明见解析;(2)BC=6.
【解析】
(1)连接OD,作OF⊥AC于F,如图,利用等腰三角形的性质得AO⊥BC,AO平分∠BAC,再根据切线的性质得OD⊥AB,然后利用角平分线的性质得到OF=OD,从而根据切线的判定定理得到结论;
(2)过D作DF⊥BC于F,连接OD,根据三角函数的定义得到![]() ,设DF=
,设DF=![]() a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到
a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
(1)证明:连接OD,OA,作OF⊥AC于F,如图,
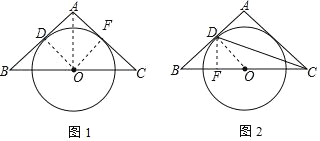
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AB与⊙O相切于点D,
∴OD⊥AB,
而OF⊥AC,
∴OF=OD,
∴AC是⊙O的切线;
(2)过D作DF⊥BC于F,连接OD,
∵tan∠BCD=![]() ,
,
∴![]() ,
,
设DF=![]() a,OF=x,则CF=4a,OC=4a﹣x,
a,OF=x,则CF=4a,OC=4a﹣x,
∵O是底边BC中点,
∴OB=OC=4a﹣x,
∴BF=OB﹣OF=4a﹣2x,
∵OD⊥AB,
∴∠BDO=90°,
∴∠BDF+∠FDO=90°,
∵DF⊥BC,
∴∠DFB=∠OFD=90°,∠FDO+∠DOF=90°,
∴∠BDF=∠DOF,
∴△DFO∽△BFD,
∴![]() ,
,
∴![]() ,
,
解得:x1=x2=a,
∵⊙O的半径为![]() ,
,
∴OD=![]() ,
,
∵DF2+FO2=DO2,
∴(![]() x)2+x2=(
x)2+x2=(![]() )2,
)2,
∴x1=x2=a=1,
∴OC=4a﹣x=3,
∴BC=2OC=6.


科目:初中数学 来源: 题型:
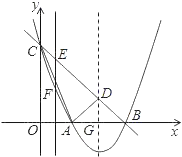
【题目】如图,顶点坐标为(2,﹣1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
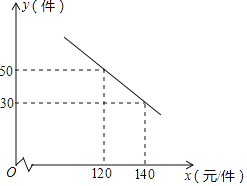
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
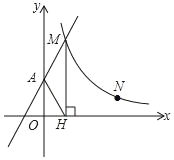
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
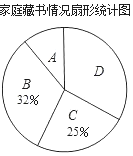
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com