
����Ŀ��ij���г����ƻ�ÿ������![]() �����г��������ڸ���ԭ��ʵ��ÿ����������ƻ�����������������죬�±��Ǹó�ijһ�ܵ�ʵ������������Լƻ�����Ϊ����������Ϊ�����������Ϊ��������λ��������
�����г��������ڸ���ԭ��ʵ��ÿ����������ƻ�����������������죬�±��Ǹó�ijһ�ܵ�ʵ������������Լƻ�����Ϊ����������Ϊ�����������Ϊ��������λ��������
���� | һ | �� | �� | �� | �� | �� | �� |
��������IJ� |
|
|
|
|
|
|
|
��![]() �����ݱ�����һ�ܸó�ʵ���������г���������
�����ݱ�����һ�ܸó�ʵ���������г���������
��![]() �����ó�ʵ����ÿ�ռƼ�����������ÿ����һ�����г��ɵ�
�����ó�ʵ����ÿ�ռƼ�����������ÿ����һ�����г��ɵ�![]() Ԫ���������������������ÿ�����⽱��
Ԫ���������������������ÿ�����⽱��![]() Ԫ����δ���������ÿ������һ����
Ԫ����δ���������ÿ������һ����![]() Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
��![]() ��������
��������![]() ���е���ÿ�ռƼ�����������Ϊ��ÿ�ܼƼ����������������������䣬�ڴ˷�ʽ�¸ó�����һ�ܵĹ����ܶ�����ÿ�ռƼ�������������Ǽ��ٻ��������ˣ����ٻ������˶��٣�
���е���ÿ�ռƼ�����������Ϊ��ÿ�ܼƼ����������������������䣬�ڴ˷�ʽ�¸ó�����һ�ܵĹ����ܶ�����ÿ�ռƼ�������������Ǽ��ٻ��������ˣ����ٻ������˶��٣�
���𰸡�(1) 848����(2) 42405Ԫ��(3)������115Ԫ.
��������
(1)���Ȱѱ���������ͣ�Ȼ�����120��7������⣻
(2)����(1)�Ľ����������֪����������ó�������һ�ܵĹ����ܶ
(3)����(1)��(2)�Ľ����������֪���������һ�ܹ��˵Ĺ����밴�ռƼ��Ĺ�����һ������.
�⣺(1)�ó�����ʵ���������г���
120��7+(+15)+(-8)+(+2)+(-12)+(-3)+(+10)+(+4)=848(��)��
(2)848��50+(15+2+10+4)��15+(-8-12-3)��20=42405(Ԫ)��
��ó�������һ�ܵĹ����ܶ���42405Ԫ��
(3)ʵ��ÿ�ܼƼ������ƵĹ���Ϊ848��50+(848-120��7)��15=42520(Ԫ)��
42520-42405=115(Ԫ)
�����ܼƼ��Ƶ�һ�ܹ���������115Ԫ.
�ʴ�Ϊ��(1) 848����(2) 42405Ԫ��(3)������115Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧУ��֯�İ��꼶֪ʶ�����У�ÿ��μӱ�����������ͬ���ɼ���Ϊ![]() ��
��![]() ��
��![]() ��
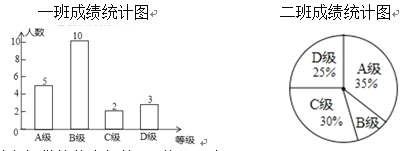
��![]() �ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֡�90�֡�80�֡�70�֣�ѧУ��һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��
�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֡�90�֡�80�֡�70�֣�ѧУ��һ��Ͷ���ijɼ����������Ƴ����µ�ͳ��ͼ��
������������ṩ����Ϣ����������⣺
��1����һ�����ѡ�ֵ�ƽ���ɼ���
��2���˴ξ����У�����ɼ���![]() �����ϣ�����
�����ϣ�����![]() �����������м��ˣ�
�����������м��ˣ�
��3����������ѡ�ֳɼ�����λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ����ı���
�ֱ����ı���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣬������˵����
���е㣬������˵����
����![]() �����ı���
�����ı���![]() Ϊ���Σ�
����
����![]() �����ı���
�����ı���![]() Ϊ���Σ�
����
�����ı���![]() ��ƽ���ı��Σ���
��ƽ���ı��Σ���![]() ��
��![]() ���ഹֱƽ�֣�
���ഹֱƽ�֣�
�����ı���![]() �������Σ���
����������![]() ��
��![]() ���ഹֱ�����.
���ഹֱ�����.
������ȷ�ĸ����ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¸�˰����2018��1��1����ʩ�У�2018��10��1����ʩ�����¡������㣺5000Ԫ����˰�ʣ����л�������������˰���еĸ�������˰˰�����£�
���� | ȫ��Ӧ��˰���ö� | ˰�ʣ����� |
1 | ������3000Ԫ�IJ��� | 3 |
2 | ����3000Ԫ��12000Ԫ�IJ��� | 10 |
3 | ����12000Ԫ��25000Ԫ�IJ��� | 20 |
���С�ȫ��Ӧ��˰���ö��ָ�ӹ��ʡ�н�������м�ȥ5000Ԫ��Ľ�������ֻ�����ϱ����ݣ�
��1����ijһ�·ݿ۳�˰������8000�������˶���˰��
��2����ijһ�·���˰��ΪmԪ��m>0��������˰ǰ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ��̣�mx2����3m��1��x+2m��2=0��
��1����֤������mȡ��ֵʱ�����̺���ʵ������
��2��������x�Ķ��κ���y=mx2����3m��1��x+2m��2��ͼ����x���������ľ���Ϊ2ʱ���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
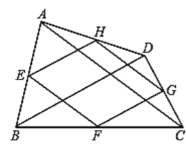
����Ŀ���û���������ͼ��ʾ�ķ�����ͼ�Σ�

��![]() �����������������ȥ����
�����������������ȥ����![]() ��ͼ���ж��ٸ���������
��ͼ���ж��ٸ���������![]() ��ͼ���أ�
��ͼ���أ�
��![]() ����
����![]() ��ͼ�����ж��ٸ����������ú�
��ͼ�����ж��ٸ����������ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��![]() �����ݣ�
�����ݣ�![]() ���н������
���н������![]() ��ͼ�����ж��ٸ�������
��ͼ�����ж��ٸ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������A��B��C�����㣬��ش�:

��1����A�������ƶ�3����λ���ȣ�C�������ƶ�5����λ���ȣ����Ǹ��Ա�ʾ�µ�ʲô����
��2���ƶ�A��B��C�е������㣬ʹ���������ʾ������ͬ���м����ƶ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������Ľ�����̣��ٽ����������
���⣺��֪ m n 100 �� x y 1 ,�� n x m y ��ֵ
�⣺ n x m y n x m y m n x y 100 1 101
���⣺��1����֪ a b 7 �� ab 10 ���� 3ab 6a 4b 2a 2ab ��ֵ��
��2����֪ a 2 2ab 2, ab b2 4, ��2a 2 ![]() ab
ab ![]() b2
b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�����˼����С���ڽⷽ���� ʱ��������һ�֡�����������Ľⷨ���ⷨ���£�
ʱ��������һ�֡�����������Ľⷨ���ⷨ���£�
�⣺�����̢�8x+20y+2y=10������Ϊ2��4x+10y��+2y=10�ۣ��ѷ��̢ٴ���۵ã�2��6+2y=10����y=-1����y=-1����ٵã�x=4�����Է�����Ľ�Ϊ��![]() ��
��
�������������⣺
��1������С���ġ�����������ķ����ⷽ����
��2����֪x��y��z������ ����z��ֵ��
����z��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com