
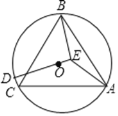
【题目】如图,△ABC为⊙O的内接等边三角形,BC=12,点D为![]() 上一动点,BE⊥OD于E,当点D由点B沿
上一动点,BE⊥OD于E,当点D由点B沿![]() 运动到点C时,线段AE的最大值是( )
运动到点C时,线段AE的最大值是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BO,取BO中点M,连接ME,点E在以M为圆心,BM为半径的圆上,由△ABC是等边三角形可得AH=BH=6,BH=6![]() ,BO=MH=4
,BO=MH=4![]() ,BM=2
,BM=2![]() ,根据勾股定理可得AM的长即
,根据勾股定理可得AM的长即
可求AE的最大值.
解:如图
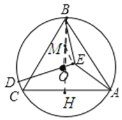
连接BO,取BO中点M,连接ME
∵DE⊥BE,M是BO中点
∴ME=![]() BO
BO
∴E在以M为圆心,BM为半径的圆上
∴当A,M,E共线且E在AM的延长线上时,AE的值最大
延长BO交AC于H
∵△ABC为⊙O的内接等边三角形
∴HB⊥AC,且△ABC是等边三角形,BC=12
∴CH=AH=6
∴AH=6 ,AO=4![]() ,BH=6
,BH=6![]()
则OM=2![]() ,MH=4
,MH=4![]()
∴AM=![]()
∴AE的最大值为2![]() +2
+2![]()
故选:A.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有两点A(﹣2,4)、B(2,4),若二次函数y=ax2﹣2ax﹣3a(a≠0)的图象与线段AB只有一个交点,则( )
A. a的值可以是![]() B. a的值可以是
B. a的值可以是![]()
C. a的值不可能是﹣1.2 D. a的值不可能是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
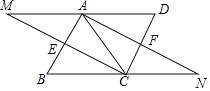
【题目】已知:如图,在平行四边形ABCD中,BC=AC,E,F分别是AB,CD的中点,连接CE并延长交DA的延长线于M,连接AF并延长交BC的延长线于N.
(1)求证:△ABN≌△CDM;
(2)当平行四边形ABCD的边或角满足什么关系时,四边形AECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了5次射击训练,平均成绩为9环,且前4次的成绩(单位:环)依次为:8,10,9,10.
(1)求甲第5次的射击成绩与这5次射击成绩的方差;
(2)乙在相同情况下也进行了5次射击训练,平均成绩为9环,方差为0.9环,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
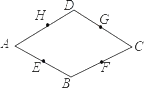
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com