Question

【题目】在△ABC中，AB=AC，∠BAC=120°，AD⊥BC，垂足为G，且AD=AB．∠EDF=60°，其两边分别交边AB，AC于点E，F．

（1）求证：△ABD是等边三角形；
（2）求证：BE=AF．

Answer 1

【答案】
（1）证明：连接BD，

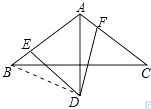
∵AB=AC，AD⊥BC，

∴∠BAD=∠DAC= ∠BAC，

∵∠BAC=120°，

∴∠BAD=∠DAC= ×120°=60°，

∵AD=AB，

∴△ABD是等边三角形

（2）证明：∵△ABD是等边三角形，

∴∠ABD=∠ADB=60°，BD=AD

∵∠EDF=60°，

∴∠BDE=∠ADF，

在△BDE与△ADF中，

，

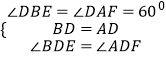∴△BDE≌△ADF（ASA），

∴BE=AF．

【解析】（1）连接BD由等腰三角形的性质和已知条件得出∠BAD=∠DAC= ×120°=60°，再由AD=AB，即可得出结论；（2）由△ABD是等边三角形，得出BD=AD，∠ABD=∠ADB=60°，证出∠BDE=∠ADF，由ASA证明△BDE≌△ADF，得出BE=AF．