
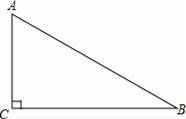
如图,已知△ABC,∠C=90°,∠B=30°.
(1)用直尺和圆规在BC上找一点D,使DA=DB.(不写作法,保留作图痕迹)
(2)若BC=8,求点D到边AB的距离.

【考点】作图—复杂作图;线段垂直平分线的性质;含30度角的直角三角形.
【分析】(1)直接利用线段垂直平分线的作法得出答案;
(2)利用线段垂直平分线的性质得出∠DAB=∠B=30°,进而得出DC=DE,再得出2DE+DE=BC,求出答案即可.
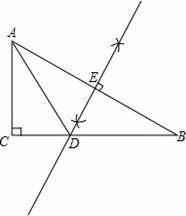
【解答】解:(1)如图所示:点D即为所求;
(2)∵DE是AB的垂直平分线,
∴AD=DB,DE⊥AB,
∴∠DAB=∠B=30°,
∵∠BAC=60°,
∴∠CAD=∠DAB=30°,
∵∠C=90°,DE⊥AB,
∴DC=DE,
∵DE⊥AB,∠B=30°,
∴BD=2DE,
∴2DE+DE=BC=8,
∴DE=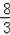
 .
.

【点评】此题主要考查了复杂作图以及线段垂直平分线的性质与作法,正确掌握线段垂直平分线的性质是解题关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
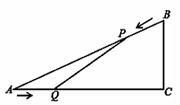
如图,在Rt△ABC中,AB=10 cm, sinA=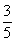 .如果点P由B出发沿BA向点A匀速运动,
.如果点P由B出发沿BA向点A匀速运动,
同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2 cm/s,点Q的速度为
1 cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5).
(1)求AC,BC的长;
(2)当t为何值时,△APQ的面积为△ABC面积的 ;
;
(3)当t为何值时,△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=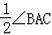
 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=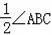
 中正确的有( )
中正确的有( )
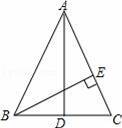

A.①② B.②③ C.①②③ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com