
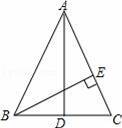
如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=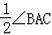
 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=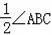
 中正确的有( )
中正确的有( )

A.①② B.②③ C.①②③ D.①②③④
A【考点】等腰三角形的判定与性质.
【分析】根据线段的垂直平分线的性质求出AB=AC,进一步求得∠BAD=∠CAD=
 ∠BAC;根据等角的余角相等即可求出∠EBC=∠DAC=
∠BAC;根据等角的余角相等即可求出∠EBC=∠DAC=
 ∠BAC;根据勾股定理即可判断③,根据∠BAC≠∠ABC,∠EBC=
∠BAC;根据勾股定理即可判断③,根据∠BAC≠∠ABC,∠EBC=
 ∠BAC,即可判断④.
∠BAC,即可判断④.
【解答】解:∵AD⊥BC垂足为点D,AD是BC边上的中线,
∴AD垂直平分BC,
∴AB=AC,∴①正确;
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=
 ∠BAC,
∠BAC,
∵BE⊥AC,AD⊥BC,
∴∠EBC+∠C=90°,∠DAC+∠C=90°,
∴∠EBC=∠DAC,
∴∠EBC=
 ∠BAC,∴②正确;
∠BAC,∴②正确;
∵AE2=AB2﹣BE2,CE2=BC2﹣BE2,AB≠BC,
∴AE≠CE,∴③错误;
∵∠BAC≠∠ABC,∠EBC=
 ∠BAC,
∠BAC,
∴∠EBC≠
 ∠ABC,∴④错误;
∠ABC,∴④错误;
∴①②都正确;
故选A.
【点评】本题考查了等腰三角形的判定和性质,等角的余角的性质和勾股定理的应用,关键是熟练地运用定理进行推理,题目比较典型,难度不大.


科目:初中数学 来源: 题型:
如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结AD,CD.则△ABC≌△ADC的依据是 .
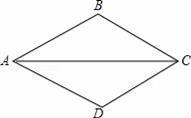

查看答案和解析>>
科目:初中数学 来源: 题型:
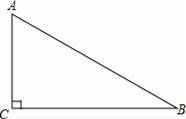
如图,已知△ABC,∠C=90°,∠B=30°.
(1)用直尺和圆规在BC上找一点D,使DA=DB.(不写作法,保留作图痕迹)
(2)若BC=8,求点D到边AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
今年小强的爷爷66岁,小强12岁 ,x年前爷爷的年龄是小强的7倍,则可列方程( )
,x年前爷爷的年龄是小强的7倍,则可列方程( )
A. 12x=66 B. 7(66-x)=12-x C. 66-x=7(12-x) D. 12x×7=66
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=10cm,则AC等于( )


A.10cm B.8cm C.5cm D.2.5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com