
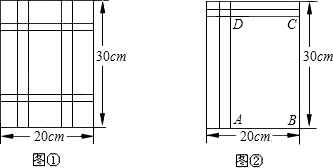
分析 因为每个竖彩条的宽为3x,图中有两个竖条,所以得到AB=20-2•3x=20-6x,又每个横彩条的宽为2x,图中有两个横条,所以BC=30-2•2x=30-4x,然后用AB•BC即为矩形ABCD的面积,从题中已知可知矩形ABCD的面积等于总体面积的$\frac{2}{3}$,根据题中的等量关系:矩形ABCD的面积=(1-$\frac{1}{3}$)×30×20,列出方程求解,再根据条件取值.
解答 解:(1)AB=(20-6x)cm,(30-4x)cm;
(2)根据题意,得24x2-260x+600=(1-$\frac{1}{3}$)×20×30,
整理,得6x2-65x+50=0,
解方程,得x1=$\frac{5}{6}$,x2=10(不合题意,舍去),
则2x=$\frac{5}{3}$,3x=$\frac{5}{2}$.
答:每个横条的宽度为$\frac{5}{3}$cm,竖彩条的宽度为$\frac{5}{2}$cm.
故答案为:(20-6x),(30-4x).
点评 考查了一元二次方程的应用,用含x的代数式正确表示矩形ABCD的长与宽是列对方程的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
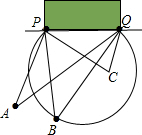 如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式.
如图,在“世界杯”足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到A点时,同样乙已经助攻冲到B点,丙助攻到C点.有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.第三种是甲将球传给丙,由丙射门.仅从射门角度考虑,应选择第三种射门方式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com