
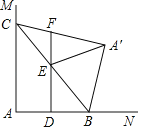
【题目】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为_____.
【答案】![]() 或2.
或2.
【解析】
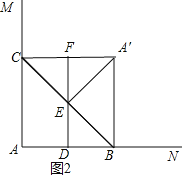
当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,根据对称的性质和平行线可得:A'C=A'E=2,根据直角三角形斜边中线的性质得:BC=2A'B=4,最后利用勾股定理可得AB的长;②当∠A'FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=2.
解:当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,
∵△A′BC与△ABC关于BC所在直线对称,
∴A'C=AC=2,∠ACB=∠A'CB,
∵点D,E分别为AB,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠BDE=∠MAN=90°,
∴∠BDE=∠A'EF,
∴AB∥A'E,
∴∠ABC=∠A'EB,
∴∠A'BC=∠A'EB,
∴A'B=A'E,
Rt△A'CB中,∵E是斜边BC的中点,
∴BC=2A'E,
由勾股定理得:AB2=BC2﹣AC2,
∴AE′=![]() ,
,
∴AB=![]() ;
;
②当∠A'FE=90°时,如图2,
∵∠ADF=∠A=∠DFC=90°,
∴∠ACF=90°,
∵△A′BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA'=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=2;
综上所述,AB的长为![]() 或2;
或2;
故答案为:![]() 或2.
或2.



科目:初中数学 来源: 题型:
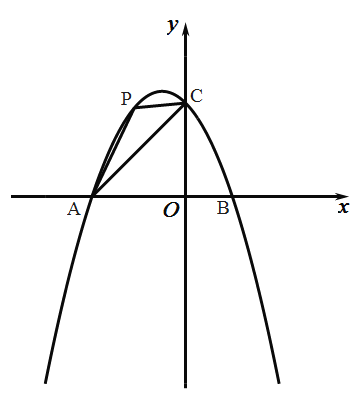
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的表达式;
(2)点![]() 是抛物线上第二象限内的点,连接
是抛物线上第二象限内的点,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
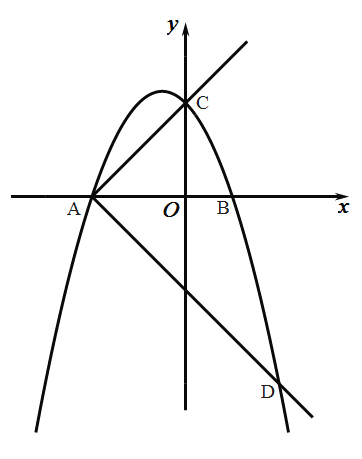
(3)作射线![]() ,将射线
,将射线![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 交抛物线于另一点
交抛物线于另一点![]() ,在射线
,在射线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小.若存在,求出
的周长最小.若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,等边
,等边![]() 的边长为
的边长为![]() ,把
,把![]() 放在
放在![]() 中,使
中,使![]() 与
与![]() 重合,点
重合,点![]() 在
在![]() 边上,如图所示,此时点
边上,如图所示,此时点![]() 是
是![]() 中点,在
中点,在![]() 内部将
内部将![]() 按下列方式旋转:绕点
按下列方式旋转:绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作,此时点
次操作,此时点![]() 是
是![]() 中点,
中点,![]() 旋转了__________
旋转了__________![]() ;再绕点
;再绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作;……这样依次绕
次操作;……这样依次绕![]() 的某个顶点连续旋转下去,第
的某个顶点连续旋转下去,第![]() 次操作完成时,
次操作完成时,![]() _____________.
_____________.
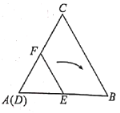
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,2),B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.

(1)请在图中描出该函数图象上另外的两个点,并画出图象;
(2)求出该二次函数的解析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
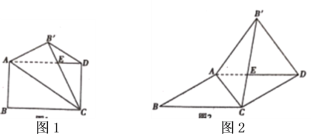
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
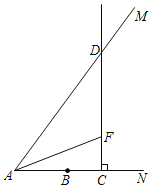
【题目】如图,射线AN上有一点B,AB=5,tan∠MAN=![]() ,点C从点A出发以每秒3个单位长度的速度沿射线AN运动,过点C作CD⊥AN交射线AM于点D,在射线CD上取点F,使得CF=CB,连结AF.设点C的运动时间是t(秒)(t>0).
,点C从点A出发以每秒3个单位长度的速度沿射线AN运动,过点C作CD⊥AN交射线AM于点D,在射线CD上取点F,使得CF=CB,连结AF.设点C的运动时间是t(秒)(t>0).
(1)当点C在点B右侧时,求AD、DF的长.(用含t的代数式表示)
(2)连结BD,设△BCD的面积为S平方单位,求S与t之间的函数关系式.
(3)当△AFD是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在
日贵州环保行活动“美丽乌江 拒绝污染”正式开启,乌江支流由于长期采磷及磷化工发展造成了总磷污染.当地政府提出五条整改措施,力求在![]() 天以内使总磷含量达标(即总磷浓度低于
天以内使总磷含量达标(即总磷浓度低于![]() ).整改过程中,总磷浓度
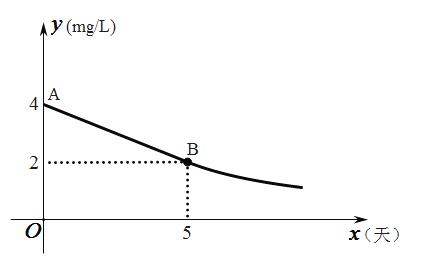
).整改过程中,总磷浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前
表示前![]() 天的变化规律,且线段
天的变化规律,且线段![]() 所在直线的表达式为:
所在直线的表达式为:![]() ,从第
,从第![]() 天起,该支流总磷浓度
天起,该支流总磷浓度![]() 与时间
与时间![]() 成反比例关系.
成反比例关系.
(1)求整改全过程中总磷浓度![]() 与时间
与时间![]() 的函数表达式;
的函数表达式;
(2)该支流中总磷的浓度能否在![]() 天以内达标?说明理由.
天以内达标?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com