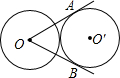练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．两个等圆⊙O和⊙O′外切，过⊙O作⊙O′的两条切线OA、OB、A、B是切点，则∠AOB等于多少度？

    分析 利用两圆的半径分别为R和r，外切时P=R+r，进而得出OO′=2O′A，即可得出∠AOO′=30°，再求出答案即可．

    解答 解：连接O′A，OO′，
    ∵过⊙O作⊙O′的两条切线OA、OB、A、B是切点，
    ∴O′A⊥OA，∠AOO′=∠BOO′，
    又∵OO′=2O′A，
    ∴∠AOO′=30°，
    ∴∠AOB=2∠AOO′=60°．

    点评 本题考查了切线的性质以及相切两圆的性质，得出OO′=2O′A是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．
    我们有多少种剪法，图1是其中的一种方法：定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．

    （1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
    （2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值；
    （3）如图3，△ABC中，AC=3，BC=4，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知：CP为圆O切线，AB为圆的割线，CP、AB交于P，求证：AP•BP=CP2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．把数-5，$-\frac{5}{2}$，0，$3\frac{1}{2}$用“＜”号从小到大连起来：-5＜$-\frac{5}{2}$＜0＜$3\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在数轴上表示下列五个数：-3，3，0.5，-1.5，-4.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

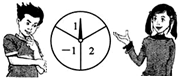    1．如图，一转盘被等分成三个扇形，上面分别标有-1，2，指针位置固定，转动转盘后任其自由停止后，某个扇形会恰好停在指针所指的位置，得到这个扇形上相应的数．若指针恰好指在等分线上，则需重新转动转盘．
    （1）若小静转动转盘一次，则她得到负数的概率为$\frac{1}{3}$；
    （2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”．请用列表法（或画树状图）求出两人“不谋而合”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

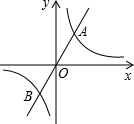    8．如图，正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A（1，2），B两点，给出下列结论：①k1＜k2；②当x＜-1时，y1＜y2；③当y1＞y2时，y2随x的增大而减小；④当x＜0时，y2随x的增大而减小．其中正确的有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．小明的爸爸买回两块地毯，他告诉小明小地毯的面积正好是大地毯面积的$\frac{1}{3}$，且两块地毯的面积和为20平方米，小明很快便得出了两块地毯的面积为（单位：平方米）（　　）
    A．$\frac{40}{3}$，$\frac{20}{3}$B．30，10C．15，5D．12，8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车速度为120千米/小时，乙车速度为80千米/小时，经过t小时两车相距50千米．则t的值是（　　）
    A．2B．2或2.25C．2.5D．2或2.5

    查看答案和解析>>

    同步练习册答案