
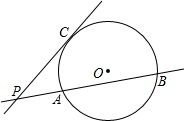
 已知:CP为圆O切线,AB为圆的割线,CP、AB交于P,求证:AP•BP=CP2.
已知:CP为圆O切线,AB为圆的割线,CP、AB交于P,求证:AP•BP=CP2. 分析 连接AC、BC、CO并延长交圆O于点M,连结AM.先由切线的性质得出OC⊥PC,那么∠ACP+∠ACM=90°,由圆周角定理及直角三角形两锐角互余得出∠M+∠ACM=90°,根据同角的余角相等得出∠ACP=∠M,由圆周角定理得出∠M=∠CBP,那么∠ACP=∠CBP,又∠APC=∠CPB,得出△ACP∽△CBP,根据相似三角形对应边成比例得到AP:CP=CP:BP,即AP•BP=CP2.
解答 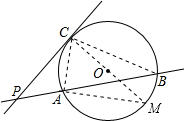 证明:连接AC、BC、CO并延长交圆O于点M,连结AM.
证明:连接AC、BC、CO并延长交圆O于点M,连结AM.
∵PC是圆O的切线,
∴OC⊥PC,
∴∠ACP+∠ACM=90°,
又∵CM是直径,
∴∠M+∠ACM=90°,
∴∠ACP=∠M,
∵∠M=∠CBP,
∴∠ACP=∠CBP,
又∵∠APC=∠CPB(公共角),
∴△ACP∽△CBP,
∴AP:CP=CP:BP,
∴AP•BP=CP2.
点评 本题实际上证明了切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.涉及到的知识点有:切线的性质,圆周角定理,直角三角形的性质,余角的性质,相似三角形的判定与性质.准确作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
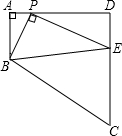 如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com