
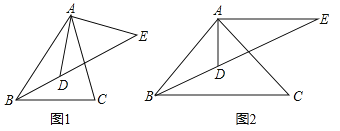
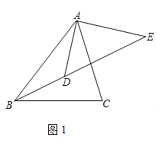
【题目】如图1,![]() 分别是
分别是![]() 的内角
的内角![]() 的平分线,过点
的平分线,过点 ![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
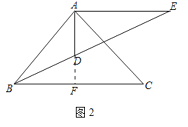
(2)如图2,如果![]() ,且
,且![]() ,求
,求![]() ;
;
(3)如果![]() 是锐角,且
是锐角,且![]() 与
与![]() 相似,求
相似,求![]() 的度数,并直接写出
的度数,并直接写出![]() 的值
的值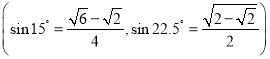 .
.
【答案】(1)证明见解析;(2)![]() ;(3)当
;(3)当![]() ,
,![]() ;当
;当![]() ,
,![]() .
.
【解析】
(1)先利用角平分线的性质,得![]() ,
, ![]() ,再利用外角、三角形内角和进行换算即可;
,再利用外角、三角形内角和进行换算即可;
(2)延长AD,构造平行相似,得到![]() ,再按条件进行计算;
,再按条件进行计算;
(3)利用△ABC与△ADE相似,得到 ![]() ,所以得到
,所以得到![]() 或
或![]() ,再利用三角函数求值.
,再利用三角函数求值.
(1)如图1中
∵![]()
∴![]() ,
,![]()
∵AD平分![]()
∴![]() ,同理得
,同理得![]()
∵![]() ,
,
![]()
∴![]()
∴![]()
(2)延长AD交BC于点F
∵![]()
∴![]()
BE平分∠ABC
∴![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
(3)∵△ABC与△ADE相似,![]()
∴∠ABC中必有一个内角和为90°
∵∠ABC是锐角
∴![]()
当![]() 时
时
∵![]()
∴![]()
∵![]()
∴![]() ,
,
∵![]() 分别是
分别是![]() 的内角
的内角![]() 的平分线
的平分线
∴![]()
∴![]()
∵![]()
∴![]()
代入解得
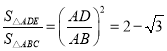
②当![]() 时
时
![]()
∵△ABC与△ADE相似
∴![]()
∵![]() 分别是
分别是![]() 的内角
的内角![]() 的平分线
的平分线
∴![]()
∴![]()
此时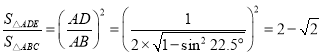
综上所述,当![]() ,
,![]() ;当
;当![]() ,
,![]()


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ABC=90°,AB=BC=2,现将Rt△ABC绕点A逆时针旋转30°得到△AED,则图中阴影部分的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年重庆国际马拉松赛于3月31日在南滨公园鸣枪开跑已知A、B两补给站之间的路程为1470米,志愿者甲、乙都从A站出发支援B站.甲先出发,且在途中停留了4分钟,甲出发6分钟后,乙才从A站出发.在整个行走过程中,两人保持各自速度匀速行走,两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达B站时,甲与B站相距的路程是_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.其中,1和0既不是质数也不是合数.数学家欧几里得在《几何原本》中对此进行过详细论述.一个较大自然数是质数还是合数通常用“N法”来判断,主要分为三个步骤:第一步,找出大于N且最接近N的平方数![]() ;第二步,用小于
;第二步,用小于![]() 的所有质数去除N;第三步,如果这些质数都不能整除N,那么N就是质数;如果这些质数中至少有一个能整除N,那么N就是合数.如判断239是质数还是合数?第一步,
的所有质数去除N;第三步,如果这些质数都不能整除N,那么N就是质数;如果这些质数中至少有一个能整除N,那么N就是合数.如判断239是质数还是合数?第一步,![]() ;第二步,小于 16的质数有: 2、3、5、7、11、13,用2、3、5、7、11、13 依次去除239;第三步,发现没有质数能整除239,所以239是质数.
;第二步,小于 16的质数有: 2、3、5、7、11、13,用2、3、5、7、11、13 依次去除239;第三步,发现没有质数能整除239,所以239是质数.
分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(a, b, c…是不相等的质数,m,n,p… 是正整数),则合数N共有
…(a, b, c…是不相等的质数,m,n,p… 是正整数),则合数N共有![]() …个约数.如
…个约数.如![]() ,
, ![]() ,则8共有4 个约数;又如
,则8共有4 个约数;又如![]() ,则12共有6个约数.
,则12共有6个约数.
请用以上方法解决下列问题:
(1)请用“ N法”判断619是质数还是合数?
(2)求有18个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的盒子.(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为900cm2,求剪掉的正方形的边长;
(2)求折成的无盖盒子的侧面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
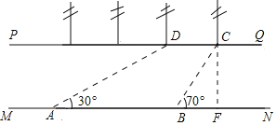
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
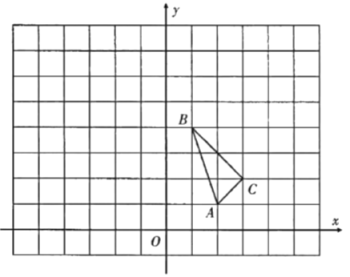
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
请解答下列问题:
(1)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(2)以原点![]() 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在![]() 轴的右侧,画出
轴的右侧,画出![]() 放大后的图形
放大后的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(3)如果点![]() 在线段
在线段![]() 上,请直接写出经过(2)的变化后对应点
上,请直接写出经过(2)的变化后对应点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com