
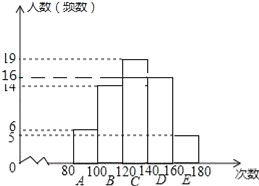
【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
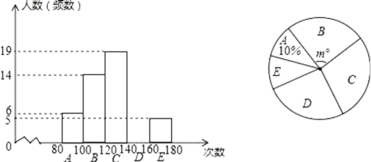
(1)补全频数分布直方图;
(2)扇形图中m= ;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
【答案】(1)见解析;(2)84;(3)2056
【解析】
(1)首先由A小组有6人,占10%,可求得总人数,再根据各小组频数之和等于数据总数求得第四小组的人数,作出统计图;
(2)360°乘以B组所占的比例,即可求出对应扇形圆心角的度数;
(3)求出样本中成绩优秀的人数所占的百分比,用样本估计总体即可.
解:(1)由直方图和扇形图可知,A组人数是6人,占10%,
则总人数:6÷10%=60(人),
D组人数为:60﹣6﹣14﹣19﹣5=16;
(2)m=360°×![]() =84°.
=84°.
故答案是:84;
(3)成绩为优秀的大约有:5900×![]() =2056(人).
=2056(人).
答:估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有2056人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
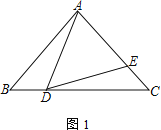
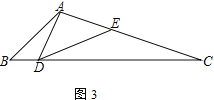
【题目】已知:△ABC中,点D为边BC上一点,点E在边AC上,且∠ADE=∠B
(1) 如图1,若AB=AC,求证:![]() ;
;
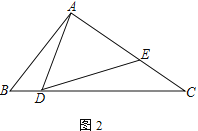
(2) 如图2,若AD=AE,求证:![]() ;
;
(3) 在(2)的条件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,则AB=____________.
,则AB=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
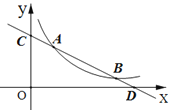
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
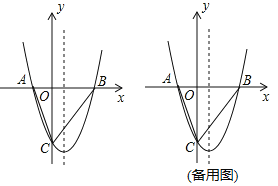
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;
(3)点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.
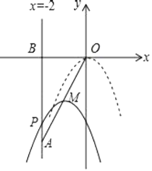
(1)线段OA所在直线的函数解析式是 ;
(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.
(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,过
的直径,过![]() 的中点
的中点![]() 作
作![]() 的直径
的直径![]() 交弦
交弦![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
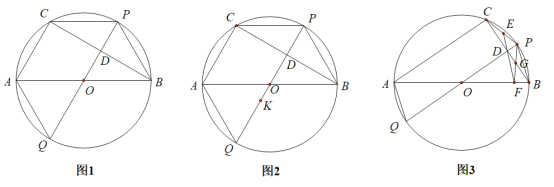
(1)如图1,若点![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 的度数;
的度数;
(2)如图2,在![]() 上取一点
上取一点![]() ,使
,使![]() ,求证:
,求证:![]() ;
;
(3)如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() 交于点
交于点![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂拟建一个如图所示的矩形仓库ABCD,仓库的一边是长为12m的一面墙,另外三边用30m长的建筑材料围成.设AB的长为xm,矩形ABCI的面积为Sm2.
(1)用含x的代数式表示BC的长,并求出x的取值范围.
(2)写出S关于x的函数关系式,并求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过P(2,2),顶点为O(0,0),将该图象向右平移,当它再次经过点P时,所得抛物线的函数表达式为( )
A.y=![]() x2B.y=
x2B.y=![]() (x﹣2)2C.y=
(x﹣2)2C.y=![]() (x﹣4)2D.y=
(x﹣4)2D.y=![]() (x﹣2)2+2
(x﹣2)2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com