
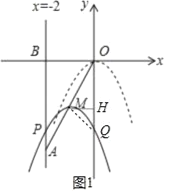
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΒψA(©¹2Θ§©¹4)Θ§÷±œΏx=©¹2”κx÷αœύΫΜ”ΎΒψBΘ§Ν§Ϋ”OAΘ§≈ΉΈοœΏy=©¹x2¥”ΒψO―ΊOAΖΫœρΤΫ“ΤΘ§”κ÷±œΏx=©¹2ΫΜ”ΎΒψPΘ§ΕΞΒψMΒΫΒψA ±ΆΘ÷Ι“ΤΕ·Θ°
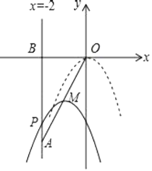
Θ®1Θ©œΏΕΈOAΥυ‘Ύ÷±œΏΒΡΚ· ΐΫβΈω Ϋ «ΓΓ ΘΜ
Θ®2Θ©…ηΤΫ“ΤΚσ≈ΉΈοœΏΒΡΕΞΒψMΒΡΚαΉχ±ξΈΣmΘ§Έ ΘΚΒ±mΈΣΚΈ÷Β ±Θ§œΏΕΈPAΉν≥ΛΘΩ≤Δ«σ≥ω¥Υ ±PAΒΡ≥ΛΘ°
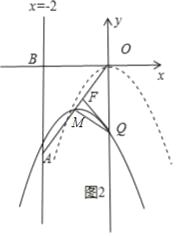
Θ®3Θ©»τΤΫ“ΤΚσ≈ΉΈοœΏΫΜy÷α”ΎΒψQΘ§ «Ζώ¥φ‘ΎΒψQ ΙΒΟΓςOMQΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©y=2xΘΜΘ®2Θ©Β±m=1 ±Θ§PAΒΡ÷ΒΉν¥σΘ§PAΒΡΉν¥σ÷ΒΈΣ1ΘΜΘ®3Θ©¥φ‘ΎΘ§(0Θ§5©¹2![]() )Μρ(0Θ§©¹8)
)Μρ(0Θ§©¹8)
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ÷±œΏOAΒΡΫβΈω ΫΘΜ
Θ®2Θ©…ηMΒψΒΡΉχ±ξΈΣΘ®mΘ§2mΘ©Θ§Θ®©¹2ΓήmΘΦ0Θ©Θ§άϊ”ΟΕΞΒψ Ϋ–¥≥ωΤΫ“ΤΚσ≈ΉΈοœΏΫβΈω ΫΈΣy=©¹Θ®x©¹mΘ©2+2mΘ§‘ρ PΒψΒΡΉχ±ξΈΣΘ®©¹2Θ§©¹m2©¹2m©¹4Θ©Θ§Υυ“‘PA=©¹m2©¹2mΘ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΫβΨωΈ ΧβΘΜ
Θ®3Θ©œ»»ΖΕ®OQ=m2©¹2mΘ§OM=©¹![]() mΘ§‘ΌΧ÷¬έΘΚΒ±OM=OQΘ§Φ¥©¹
mΘ§‘ΌΧ÷¬έΘΚΒ±OM=OQΘ§Φ¥©¹![]() m=m2©¹2mΘ§»ΜΚσΫβΖΫ≥Χ«σ≥ωmΦ¥Ω…ΒΟΒΫ¥Υ ±QΒψΉχ±ξΘΜΒ±OM=MQΘ§ΉςMHΓΆOQ”ΎHΘ§»γΆΦ1Θ§άϊ”ΟOH=QHΒΟΒΫ©¹2m=m2©¹2m©¹Θ®©¹2mΘ©Θ§»ΜΚσΫβΖΫ≥Χ«σ≥ωmΦ¥Ω…ΒΟΒΫQΒψΉχ±ξΘΜΒ±QM=QOΘ§ΉςQFΓΆOM”ΎFΘ§»γΆΦ2Θ§‘ρOF=MF=©¹
m=m2©¹2mΘ§»ΜΚσΫβΖΫ≥Χ«σ≥ωmΦ¥Ω…ΒΟΒΫ¥Υ ±QΒψΉχ±ξΘΜΒ±OM=MQΘ§ΉςMHΓΆOQ”ΎHΘ§»γΆΦ1Θ§άϊ”ΟOH=QHΒΟΒΫ©¹2m=m2©¹2m©¹Θ®©¹2mΘ©Θ§»ΜΚσΫβΖΫ≥Χ«σ≥ωmΦ¥Ω…ΒΟΒΫQΒψΉχ±ξΘΜΒ±QM=QOΘ§ΉςQFΓΆOM”ΎFΘ§»γΆΦ2Θ§‘ρOF=MF=©¹![]() mΘ§÷ΛΟςRtΓςOFQΓΉRtΓςABOΘ§άϊ”ΟœύΥΤ±»ΒΟΒΫ
mΘ§÷ΛΟςRtΓςOFQΓΉRtΓςABOΘ§άϊ”ΟœύΥΤ±»ΒΟΒΫ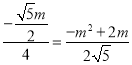 Θ§ΫβΒΟm≤Μ¬ζΉψΧθΦΰ…α»ΞΘ°
Θ§ΫβΒΟm≤Μ¬ζΉψΧθΦΰ…α»ΞΘ°
ΫβΘΚΘ®1Θ©…η÷±œΏOAΒΡΫβΈω ΫΈΣy=kxΘ§
Α―Θ®©¹2Θ§©¹4Θ©¥ζ»κΒΟ©¹2k=©¹4Θ§ΫβΒΟk=2Θ§
Υυ“‘÷±œΏOAΒΡΫβΈω ΫΈΣy=2xΘΜ
Ι ¥πΑΗΈΣy=2xΘΜ
Θ®2Θ©…ηMΒψΒΡΉχ±ξΈΣΘ®mΘ§2mΘ©Θ§Θ®©¹2ΓήmΘΦ0Θ©Θ§
ΓύΤΫ“ΤΚσ≈ΉΈοœΏΫβΈω ΫΈΣy=©¹Θ®x©¹mΘ©2+2mΘ§
Β±x=©¹2 ±Θ§y=©¹Θ®2©¹mΘ©2+2m=©¹m2©¹2m©¹4Θ§
ΓύPΒψΒΡΉχ±ξΈΣΘ®©¹2Θ§©¹m2©¹2m©¹4Θ©Θ§
ΓύPA=©¹m2©¹2m©¹4©¹Θ®©¹4Θ©=©¹m2©¹2m=©¹Θ®m©¹1Θ©2+1
ΓύΒ±m=1 ±Θ§PAΒΡ÷ΒΉν¥σΘ§PAΒΡΉν¥σ÷ΒΈΣ1ΘΜ
Θ®3Θ©¥φ‘ΎΘ§άμ”…»γœ¬ΘΚ
Β±x=0 ±Θ§y=©¹Θ®0©¹mΘ©2+2m=©¹m2+2mΘ§‘ρQΘ®0Θ§©¹m2+2mΘ©Θ§
ΓΏOQ=m2©¹2mΘ§OM=©¹![]() mΘ§
mȧ
Β±OM=OQΘ§Φ¥©¹![]() m=m2©¹2mΘ§Φ¥m2©¹Θ®2©¹
m=m2©¹2mΘ§Φ¥m2©¹Θ®2©¹![]() Θ©m=0Θ§ΫβΒΟm1=0Θ®…α»ΞΘ©Θ§m2=2©¹
Θ©m=0Θ§ΫβΒΟm1=0Θ®…α»ΞΘ©Θ§m2=2©¹![]() Θ§¥Υ ±QΒψΉχ±ξΈΣΘ®0Θ§5©¹2
Θ§¥Υ ±QΒψΉχ±ξΈΣΘ®0Θ§5©¹2![]() Θ©ΘΜ
Θ©ΘΜ
Β±OM=MQΘ§ΉςMHΓΆOQ”ΎHΘ§»γΆΦ1Θ§‘ρOH=QHΘ§©¹2m=m2©¹2m©¹Θ®©¹2mΘ©Θ§Φ¥m2+2m=0Θ§ΫβΒΟm1=0Θ®…α»ΞΘ©Θ§m2=©¹2Θ§¥Υ ±QΒψΉχ±ξΈΣΘ®0Θ§©¹8Θ©ΘΜ
Β±QM=QOΘ§ΉςQFΓΆOM”ΎFΘ§»γΆΦ2Θ§‘ρOF=MF=©¹![]() mΘ§
mȧ
ÿOQøABȧ
ΓύΓœQOF=ΓœBAOΘ§
ΓύRtΓςOFQΓΉRtΓςABOΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥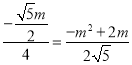 Θ§’ϊάμΒΟ4m2©¹3m=0Θ§ΫβΒΟm1=0Θ®…α»ΞΘ©Θ§m2=
Θ§’ϊάμΒΟ4m2©¹3m=0Θ§ΫβΒΟm1=0Θ®…α»ΞΘ©Θ§m2=![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡQΒψΉχ±ξΈΣΘ®0Θ§5©¹2![]() Θ©ΜρΘ®0Θ§©¹8Θ©Θ°
Θ©ΜρΘ®0Θ§©¹8Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≈©≥ΓΫώΡξΒΎ“ΜΦΨΕ»ΒΡ≤ζ÷ΒΈΣ50Άρ‘ΣΘ§ΒΎΕΰΦΨΕ»”…”ΎΗΡΫχΝΥ…ζ≤ζΖΫΖ®Θ§≤ζ÷ΒΧαΗΏΝΥ![]() ΘΜΒΪ‘ΎΫώΡξΒΎ»ΐΓΔΒΎΥΡΦΨΕ» ±ΗΟ≈©≥Γ“ρΙήάμ≤Μ…Τ.ΒΦ÷¬ΤδΒΎΥΡΦΨΕ»ΒΡ≤ζ÷Β”κΒΎΕΰΦΨΕ»ΒΡ≤ζ÷Βœύ±»œ¬ΫΒΝΥ11.4Άρ‘Σ.
ΘΜΒΪ‘ΎΫώΡξΒΎ»ΐΓΔΒΎΥΡΦΨΕ» ±ΗΟ≈©≥Γ“ρΙήάμ≤Μ…Τ.ΒΦ÷¬ΤδΒΎΥΡΦΨΕ»ΒΡ≤ζ÷Β”κΒΎΕΰΦΨΕ»ΒΡ≤ζ÷Βœύ±»œ¬ΫΒΝΥ11.4Άρ‘Σ.
Θ®1Θ©«σΗΟ≈©≥Γ‘ΎΒΎΕΰΦΨΕ»ΒΡ≤ζ÷ΒΘΜ
Θ®2Θ©«σΗΟ≈©≥Γ‘ΎΒΎ»ΐΓΔΒΎΥΡΦΨΕ»≤ζ÷ΒΒΡΤΫΨυœ¬ΫΒΒΡΑΌΖ÷¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΟϊΕ”‘±≤ΈΦ”…δΜς―ΒΝΖΘ§≥…Φ®Ζ÷±π±Μ÷Τ≥…œ¬Ν–ΝΫΗωΆ≥ΦΤΆΦΘΚ
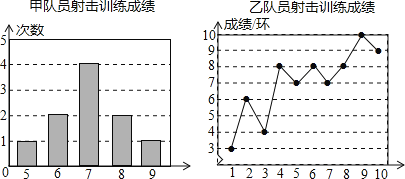
ΗυΨί“‘…œ–≈œΔΘ§’ϊάμΖ÷Έω ΐΨί»γœ¬ΘΚ
ΤΫΨυ≥…Φ®/ΜΖ | ÷–ΈΜ ΐ/ΜΖ | ÷Ύ ΐ/ΜΖ | ΖΫ≤ν | |
ΦΉ | a | 7 | 7 | 1.2 |
““ | 7 | b | 8 | c |
Θ®1Θ©–¥≥ω±μΗώ÷–aΘ§bΘ§cΒΡ÷ΒΘΚaΘΫΓΓ ΓΓΘ§bΘΫΓΓ ΓΓΘ§cΘΫΓΓ ΓΓΘ°
Θ®2Θ©»γΙϊ““‘Ό…δΜς“Μ¥ΈΘ§Οϋ÷–7ΜΖΘ§Ρ«Ο¥““ΒΡ…δΜς≥…Φ®ΒΡΖΫ≤νΓΓ ΓΓΘ°Θ®ΧνΓΑ±δ¥σΓ±ΓΑ±δ–ΓΓ±ΓΑ≤Μ±δΓ±Θ©
Θ®3Θ©ΫΧΝΖΗυΨί’β10¥Έ≥…Φ®»τ―Γ‘ώΦΉ≤ΈΦ”±»»ϋΘ§ΫΧΝΖΒΡάμ”… « ≤Ο¥ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΖΰΉΑΒξ“ρΈΣΜΜΦΨΗϋ–¬Θ§≤…ΙΚΝΥ“Μ≈ζ–¬ΖΰΉΑΘ§”–AΓΔBΝΫ÷÷Ων ΫΙ≤100ΦΰΘ§Μ®Ζ―ΝΥ6600‘ΣΘ§“―÷ΣA÷÷Ων ΫΒΞΦέ «80‘Σ/ΦΰΘ§B÷÷Ων ΫΒΡΒΞΦέ «40‘Σ/Φΰ
Θ®1Θ©«σΝΫ÷÷Ων ΫΒΡΖΰΉΑΗς≤…ΙΚΝΥΕύ…ΌΦΰΘΩ
Θ®2Θ©»γΙϊΝμ“ΜΗωΖΰΉΑΒξ“≤œκ“Σ≤…ΙΚ’βΝΫ÷÷Ων ΫΒΡΖΰΉΑΙ≤60ΦΰΘ§«“≤…ΙΚΖΰΉΑΒΡΖ―”Ο≤Μ≥§Ιΐ3300‘ΣΘ§Ρ«Ο¥A÷÷Ων ΫΒΡΖΰΉΑΉνΕύΡή≤…ΙΚΕύ…ΌΦΰΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΧε”ΐ÷–ΩΦ«ΑΘ§≥ι―υΒς≤ιΝΥΨ≈ΡξΦΕ―ß…ζΒΡΓΑ1Ζ÷÷”Χχ…ΰΓ±≥…Φ®Θ§≤ΔΜφ÷Τ≥…ΝΥœ¬ΟφΒΡΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ®ΟΩ–ΓΉιΚ§Ήν–Γ÷ΒΘ§≤ΜΚ§Ήν¥σ÷ΒΘ©ΚΆ…»–ΈΆΦΘ°
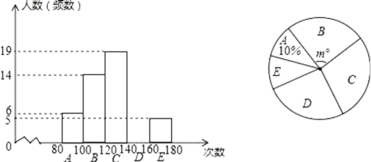
Θ®1Θ©≤Ι»ΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®2Θ©…»–ΈΆΦ÷–m=ΓΓ ΓΓΘΜ
Θ®3Θ©»τΓΑ1Ζ÷÷”Χχ…ΰΓ±≥…Φ®¥σ”ΎΜρΒ»”Ύ140¥ΈΈΣ”≈–ψΘ§‘ρΙάΦΤ»Ϊ –Ψ≈ΡξΦΕ5900Οϊ―ß…ζ÷–ΓΑ1Ζ÷÷”Χχ…ΰΓ±≥…Φ®ΈΣ”≈–ψΒΡ¥σ‘Φ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ”≠Ϋ”2020Ρξ÷–ΩΦΘ§Ρ≥÷–―ßΕ‘»Ϊ–ΘΨ≈ΡξΦΕ―ß…ζΫχ––ΝΥ“Μ¥Έ ΐ―ßΤΎΡ©ΡΘΡβΩΦ ‘Θ§≤ΔΥφΜζ≥ι»ΓΝΥ≤ΩΖ÷―ß…ζΒΡ≤β ‘≥…Φ®ΉςΈΣ―υ±ΨΫχ––Ζ÷ΈωΘ§Μφ÷Τ≥…ΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΡψΗυΨίΆ≥ΦΤΆΦ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
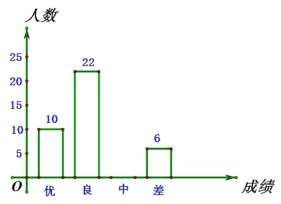
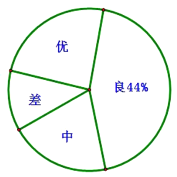
Θ®1Θ©‘Ύ’β¥ΈΒς≤ι÷–Θ§“ΜΙ≤Βς≤ιΝΥΕύ…ΌΟϊ―ß…ζΘΜ
Θ®2Θ©ΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»τΗΟ÷–―ßΨ≈ΡξΦΕΙ≤”–860»Υ≤ΈΦ”ΝΥ’β¥Έ ΐ―ßΩΦ ‘Θ§ΙάΦΤΗΟ–ΘΨ≈ΡξΦΕΙ≤”–Εύ…ΌΟϊ―ß…ζΒΡ ΐ―ß≥…Φ®Ω…“‘¥οΒΫ”≈–ψΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§≈ΉΈοœΏ![]() Θ®
Θ®![]() ΈΣ≥Θ ΐΘ©Θ°
ΈΣ≥Θ ΐΘ©Θ°
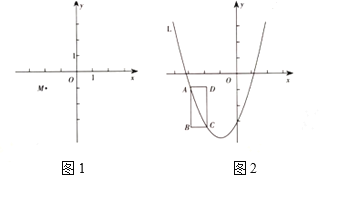
Θ®1Θ©≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΈΣ( Θ§ )Θ®”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
ΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©»τ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() «“”κ
«“”κ![]() ΆΦœσΫΜΒψΒΡΉίΉχ±ξΈΣ3Θ§«κ‘ΎΆΦ1÷–Μ≠≥ω≈ΉΈοœΏ
ΆΦœσΫΜΒψΒΡΉίΉχ±ξΈΣ3Θ§«κ‘ΎΆΦ1÷–Μ≠≥ω≈ΉΈοœΏ![]() ΒΡΦρΆΦΘ§≤Δ«σ
ΒΡΦρΆΦΘ§≤Δ«σ![]() ΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©»γΆΦ2Θ§ΙφΨΊ![]() ΒΡΥΡΧθ±ΏΖ÷±πΤΫ––”ΎΉχ±ξ÷αΘ§
ΒΡΥΡΧθ±ΏΖ÷±πΤΫ––”ΎΉχ±ξ÷αΘ§![]() Θ§»τ≈ΉΈοœΏ
Θ§»τ≈ΉΈοœΏ![]() Ψ≠Ιΐ
Ψ≠Ιΐ![]() ΝΫΒψΘ§«“ΨΊ–Έ
ΝΫΒψΘ§«“ΨΊ–Έ![]() ‘ΎΤδΕ‘≥Τ÷αΒΡΉσ≤ύΘ§‘ρΕ‘Ϋ«œΏ
‘ΎΤδΕ‘≥Τ÷αΒΡΉσ≤ύΘ§‘ρΕ‘Ϋ«œΏ![]() ΒΡΉν–Γ÷Β « Θ°
ΒΡΉν–Γ÷Β « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫax2+bx+cΒΡΕΞΒψΉχ±ξΈΣΘ®1Θ§2Θ©Θ§Ρ«Ο¥œ¬Ν–Ϋα¬έ÷–ΘΚΔΌabcΘΨ0ΘΜΔΎ2a+b®T0ΘΜΔέb2©¹4acΘΨ0ΘΜΔή»τΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+c©¹mΘΫ0ΟΜ”– Β ΐΗυΘ§‘ρmΘΨ2ΘΜΔίΖΫ≥Χ|ax2+bx+c|ΘΫ1”–ΥΡΗωΗυΘ§‘ρ’βΥΡΗωΗυΒΡΚΆΈΣ4Θ°’ΐ»ΖΒΡΗω ΐΈΣΘ®ΓΓΓΓΘ©
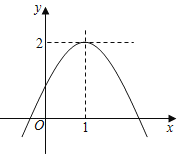
A.2ΗωB.3ΗωC.4ΗωD.5Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏlΘΚyΘΫkx+1Θ®kΓΌ0Θ©”κ÷±œΏxΘΫkΘ§÷±œΏyΘΫ©¹kΖ÷±πΫΜ”ΎΒψAΓΔBΘ§÷±œΏxΘΫk”κ÷±œΏyΘΫ©¹kΫΜ”ΎΒψCΘ§
Θ®1Θ©«σ÷±œΏl”κy÷αΒΡΫΜΒψΉχ±ξΘΜ
Θ®2Θ©ΚαΓΔΉίΉχ±ξΕΦ «’ϊ ΐΒΡΒψΫ–Ήω’ϊΒψΘ°Φ«œΏΕΈABΓΔBCΓΔCAΈß≥…ΒΡ«χ”ρΘ®≤ΜΚ§±ΏΫγΘ©ΈΣWΘ°
ΔΌΒ±kΘΫ1 ±Θ§«χ”ρΡΎΒΡ’ϊΒψ”–ΓΓ ΓΓΗωΘ§ΤδΉχ±ξΈΣΓΓ ΓΓΘ°
ΔΎΒ±kΘΫ2 ±Θ§«χ”ρWΡΎΒΡ’ϊΒψ”–ΓΓ ΓΓΗωΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com