
 ⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证:
⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证: |
| BC |
 |
| BD |
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
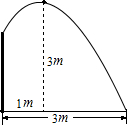 要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.
要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com