
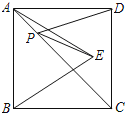
����Ŀ����ͼ1��������y=ax2+bx+3��x�ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C������AC����
��1�������������y=ax2+bx+3�Ľ���ʽ��
��2����ͼ2����P����Qͬʱ�ӵ�A��������P��AC��ÿ��![]() ����λ���ȵ��ٶȣ��ɵ�A���C�˶�����Q��AB��ÿ��2����λ���ȵ��ٶȣ��ɵ�A���B�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������P���˶�ʱ��Ϊt�룬����PQ��
����λ���ȵ��ٶȣ��ɵ�A���C�˶�����Q��AB��ÿ��2����λ���ȵ��ٶȣ��ɵ�A���B�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶������P���˶�ʱ��Ϊt�룬����PQ��
����֤��PQ��AC��
�ڹ���Q��QE��x�ᣬ���������ڵ�E������PE����PQ=PEʱ�������t��ֵ��
����y�����Ƿ���ڵ�D��ʹ�Ե�A��P��Q��DΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д��D�����꣺�������ڣ���˵�����ɣ�

���𰸡���1��y=��x2��2x+3����2���ټ���������t��ֵΪ![]() ����D��0��1����
����D��0��1����
��������
(1)�ô���ϵ������������ʽ����2����֤����OACΪ����ֱ�������Σ���֤��APQ�ס�AOC������APQ=��AOC=90�㣬����PQ��AC������PF��x����F��PH��EQ��H�����E��2t��3��2t������E��2t��3��2t������y=��x2��2x+3�é���2t��3��2��2��2t��3��+3=3���ⷽ�̿ɵã��۽⣺���ڣ����ı���AQDPΪƽ���ı��Σ���DQ=AP=![]() t����DQO=��PAQ=45�㣬��OQ=OD=3��2t���ɵ�
t����DQO=��PAQ=45�㣬��OQ=OD=3��2t���ɵ�![]() t=
t=![]() ��3��2t�������t=1���ɵ�D������.
��3��2t�������t=1���ɵ�D������.
��1���⣺�������߽���ʽΪy=a��x+3����x��1����
��y=ax2+2ax��3a��
�ੁ3a=3�����a=��1��
�������߽���ʽΪy=��x2��2x+3��
��2����֤������x=0ʱ��y=��x2��2x+3=3����C��0��3����
���OACΪ����ֱ�������Σ�
��AC=3![]() ��
��
��AP=![]() t��AQ=2t��
t��AQ=2t��
��![]() =
=![]() t��
t��![]() =
=![]() =
=![]() t��
t��
��![]() =
=![]() ��
��
����PAQ=��OAC��
���APQ�ס�AOC��
���APQ=��AOC=90�㣬
��PQ��AC��
��֤������PF��x����F��PH��EQ��H����ͼ2����PF=AF=![]() AP=
AP=![]()
![]() t=t��
t=t��
��Q��OA�ϣ�OQ=3��2t����Q��2t��3��0����H��2t��3��t����
��Q����OB�ϣ�OQ=2t��3����Q��2t��3��0����H��2t��3��t����
��PE=PQ��
��EH=QH=t��
��E��2t��3��2t����
��E��2t��3��2t������y=��x2��2x+3�é���2t��3��2��2��2t��3��+3=3�����t1=0����ȥ����t2=![]() ��
��
��t��ֵΪ![]() ��
��
�۽⣺���ڣ�
��ͼ3�����ı���AQDPΪƽ���ı��Σ�
��DQ=AP=![]() t����DQO=��PAQ=45�㣬
t����DQO=��PAQ=45�㣬
��OQ=OD=3��2t��
��![]() t=
t=![]() ��3��2t�������t=1��
��3��2t�������t=1��
��D��0��1����


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y��kx+b��ͼ����x�ᣬy��ֱ��ڵ㣨2��0�����㣨0��3���������н��ۣ���ͼ���㣨1����3����������x�ķ���kx+b��0�Ľ�Ϊx��2��������x�ķ���kx+b��3�Ľ�Ϊx��0������x��2ʱ��y��0��������ȷ���ǣ�������

A.�٢ڢ�B.�٢ۢ�C.�ڢۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�С�O�ڵ�C��AB��Բ��O����O�ڵ�B��D����AC=BC������O�İ뾶Ϊ2��ͼ����Ӱ���ֵ����Ϊ _____________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�����Ϊ64����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���AC����һ��P��ʹPD+PE�ĺ���С���������СֵΪ��������
A.6B.8C.9D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����BAC��ƽ������BC�Ĵ�ֱƽ�����ཻ�ڵ�D��DE��AB��DF��AC������ֱ�ΪE��F��AB��6��AC��4����BE��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OAB�У�C��OA���е㣬CD��OA��CD�뻡AB���ڵ�D����OΪԲ�ģ�OC�ij�Ϊ�뾶����CE��OB�ڵ�E����OA=6����AOB=120������ͼ����Ӱ���ֵ����Ϊ_________����������У���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ������ӡ���ǿ���ԡ���Ŀ�У����ذٶȴ��Ե�С�Ȼ�������3��1����ս����ն��2017��������۷�Ծ��Ľ����ʸ��˹�����ʱ���Ѿ����������
ij�̳���һ����11000Ԫ����ij��ƴװ�����˽������ۣ��ܿ�����һ�գ��̼�����24000Ԫ�ڶ��ι���ͬ������ˣ������������ǵ�һ�ε�2���������۹���10Ԫ��
��1������̼ҵ�һ�ι��������˶��ٸ���
��2�������л����˶�����ͬ�ı�����ۣ�Ҫ��ȫ��������ϵ������ʲ�����20%���������������أ�����ôÿ�������˵ı�������Ƕ���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����붬�����յ��ٴ�ӭ������������ij�̳���![]() Ԫ����һ���յ����ÿյ�����Ӧ���̼�����
Ԫ����һ���յ����ÿյ�����Ӧ���̼�����![]() Ԫ�����ڶ������ֿյ������������ȵ�һ������������
Ԫ�����ڶ������ֿյ������������ȵ�һ������������![]() ̨���������ǵ�һ����
̨���������ǵ�һ����![]() ��.
��.
(1)���̳�������һ���յ��ĵ��۶���Ԫ��
(2)�������յ�����ͬ�ı�۳��ۣ����ڽ�������ʣ��![]() ̨�յ�δ���ۣ�Ϊ���ٿ������ʽ��̼Ҿ�������
̨�յ�δ���ۣ�Ϊ���ٿ������ʽ��̼Ҿ�������![]() ̨�յ������۳��ۣ���������յ�ȫ�����������ʲ�����
̨�յ������۳��ۣ���������յ�ȫ�����������ʲ�����![]() (��������������)����ôÿ̨�յ��ı�����ٶ���Ԫ��
(��������������)����ôÿ̨�յ��ı�����ٶ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ��
(1)������ABC����y��ԳƵġ�A��B��C������д����A��B��C���������������.
(2)ֱ��д����ABC�����Ϊ______.
(3)��x���ϻ�����P��ʹPA+PC��С.(��д������������ͼ�ۼ�)

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com