
【题目】如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.

(1)求抛物线的解析式;
(2)问:当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标;
(4)设抛物线顶点为M,连接BP,BM,MQ,问:是否存在t的值,使以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
【答案】(1)y=-x2+2x+3;(2)t=1或t=![]() ;(3)点F的坐标为(2,3).(4)
;(3)点F的坐标为(2,3).(4)![]() .
.
【解析】
试题(1)先由直线AB的解析式为y=-x+3,求出它与x轴的交点A、与y轴的交点B的坐标,再将A、B两点的坐标代入y=-x2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)由直线与两坐标轴的交点可知:∠QAP=45°,设运动时间为t秒,则QA=![]() t,PA=3-t,然后再图①、图②中利用特殊锐角三角函数值列出关于t的方程求解即可;
t,PA=3-t,然后再图①、图②中利用特殊锐角三角函数值列出关于t的方程求解即可;
(3)设点P的坐标为(t,0),则点E的坐标为(t,-t+3),则EP=3-t,点Q的坐标为(3-t,t),点F的坐标为(3-t,-(3-t)2+2(3-t)+3),则FQ=3t-t2,EP∥FQ,EF∥PQ,所以四边形为平行线四边形,由平行四边形的性质可知EP=FQ,从而的到关于t的方程,然后解方程即可求得t的值,然后将t=1代入即可求得点F的坐标;
(4)设运动时间为t秒,则OP=t,BQ=(3-t)![]() ,然后由抛物线的解析式求得点M的坐标,从而可求得MB的长度,然后根据相似相似三角形的性质建立关于t的方程,然后即可解得t的值.
,然后由抛物线的解析式求得点M的坐标,从而可求得MB的长度,然后根据相似相似三角形的性质建立关于t的方程,然后即可解得t的值.
试题解析:(1)∵y=-x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=3,即A点坐标为(3,0),
当x=0时,y=3,即B点坐标为(0,3),
将A(3,0),B(0,3)代入y=-x2+bx+c,
得![]() ,解得
,解得![]()
∴抛物线的解析式为y=-x2+2x+3;
(2)∵OA=OB=3,∠BOA=90°,
∴∠QAP=45°.
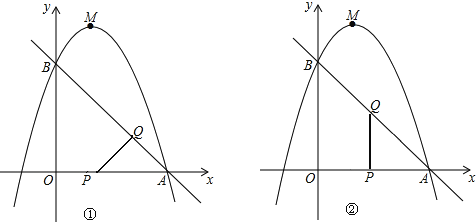
如图①所示:∠PQA=90°时,设运动时间为t秒,则QA=![]() t,PA=3-t.
t,PA=3-t.
在Rt△PQA中,![]() ,即:
,即:![]() ,解得:t=1;
,解得:t=1;
如图②所示:∠QPA=90°时,设运动时间为t秒,则QA=![]() t,PA=3-t.
t,PA=3-t.
在Rt△PQA中,![]() ,即:
,即:![]() ,解得:t=
,解得:t=![]() .
.
综上所述,当t=1或t=![]() 时,△PQA是直角三角形;
时,△PQA是直角三角形;
(3)如图③所示:
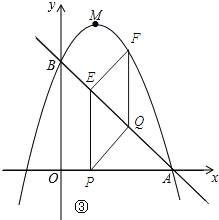
设点P的坐标为(t,0),则点E的坐标为(t,-t+3),则EP=3-t,点Q的坐标为(3-t,t),点F的坐标为(3-t,-(3-t)2+2(3-t)+3),则FQ=3t-t2.
∵EP∥FQ,EF∥PQ,
∴EP=FQ.即:3-t=3t-t2.
解得:t1=1,t2=3(舍去).
将t=1代入F(3-t,-(3-t)2+2(3-t)+3),得点F的坐标为(2,3).
(4)如图④所示:
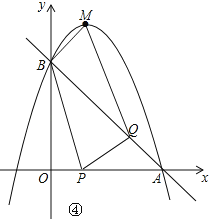
设运动时间为t秒,则OP=t,BQ=(3-t)![]() .
.
∵y=-x2+2x+3=-(x-1)2+4,
∴点M的坐标为(1,4).
∴MB=![]() .
.
当△BOP∽△QBM时,![]() 即:
即:![]() ,整理得:t2-3t+3=0,
,整理得:t2-3t+3=0,
△=32-4×1×3<0,无解:
当△BOP∽△MBQ时,![]() 即:
即:![]() ,解得t=
,解得t=![]() .
.
∴当t=![]() 时,以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似.
时,以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
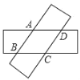
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
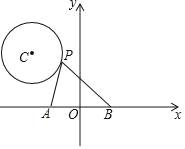
【题目】如图,在平面直角坐标系中,点P是以C(﹣![]() ,
,![]() )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而减小;⑤2a﹣b=0;⑥b2﹣4ac>0.下列结论一定成立的是( )
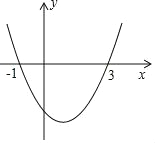
A. ①②④⑥ B. ①②③⑥ C. ②③④⑤⑥ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() 有下列说法:①如果m=2,则y有最小值3;②如果当x=1时的函数值与x=2018时的函数值相等,则当x=2019时的函数值是3;③如果m>0,则当
有下列说法:①如果m=2,则y有最小值3;②如果当x=1时的函数值与x=2018时的函数值相等,则当x=2019时的函数值是3;③如果m>0,则当![]() 时y随x的增大而减小,则
时y随x的增大而减小,则![]() ④如果该二次函数有最小值T,则T的最大值是1,其中正确的说法是________.
④如果该二次函数有最小值T,则T的最大值是1,其中正确的说法是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.

(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校举办的“弘扬社会主义核心价值观”为主题的演讲比赛中,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某特产专卖店的销售某种特产,其进价为每千克40元,若按每千克60元出售,则平均每天可售出100千克,后来经过市场调查发现,单价每降低3元,平均每天的销售量增加30千克,若专卖店销售这种特产想要平均每天获利2240元,且销量尽可能大,则每千克特产应定价多少元?
(1)方法1:设每千克特产应降价x元,由题意,得方程为:___.
方法2:设每千克特产降价后定价为x元,由题意,得方程为:___.
(2)请你选择一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式是![]() ,直线l2的解析式是
,直线l2的解析式是![]() ,点A1在l1上,A1的横坐标为
,点A1在l1上,A1的横坐标为![]() ,作
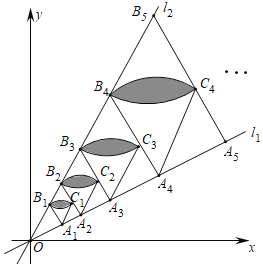
,作![]() 交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则
交l2于点B1,点B2在l2上,以B1A1,B1B2为邻边在直线l1,l2间作菱形A1B1B2C1,分别以点A1,B2为圆心,以A1B1为半径画弧得扇形B1A1C1和扇形B1B2C1,记扇形B1A1C1与扇形B1B2C1重叠部分的面积为S1;延长B2C1交l1于点A2,点B3在l2上,以B2A2,B2B3为邻边在l1,l2间作菱形A2B2B3C2,分别以点A2,B3为圆心,以A2B2为半径画弧得扇形B2A2C2和扇形B2B3C2,记扇形B2A2C2与扇形B2B3C2重叠部分的面积为S2……按照此规律继续作下去,则![]() ________.(用含有正整数n的式子表示)
________.(用含有正整数n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com