
【题目】已知![]() 是边长为
是边长为![]() 的等边三角形,点
的等边三角形,点![]() 是射线
是射线![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() .
.

(1)如图1,猜想![]() 是什么三角形? ______;(直接写出结果)
是什么三角形? ______;(直接写出结果)
(2)如图2,猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)当![]() 为何值时,
为何值时,![]() ,请说明理由.
,请说明理由.
【答案】(1)等边三角形;(2)AC+CD=CE,理由见详解;(3)BD为2或8时,∠DEC=30°,理由见详解.
【解析】
(1)根据旋转的性质得到AD=AE,∠DAE=60°,根据等边三角形的判定定理解答;
(2)证明△ABD≌△ACE,根据全等三角形的性质得到BD=CE,结合图形计算即可;
(3)根据题意,分为点D在线段BC上和点D在线段BC的延长线上两种情况,根据直角三角形的性质解答;
解:(1)由旋转变换的性质可知,AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
故答案为:等边三角形;
(2)AC+CD=CE,
证明:由旋转的性质可知,∠DAE=60°,AD=AE,
∵△ABC是等边三角形
∴AB=AC=BC,∠BAC=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS)
∴BD=CE,
∴CE=BD=CB+CD=CA+CD;
(3)BD为2或8时,∠DEC=30°,
当点D在线段BC上时,

∵∠DEC=30°,∠AED=60°,
∴∠AEC=90°,
∵△ABD≌△ACE,
∴∠ADB=∠AEC=90°,又∠B=60°,
∴∠BAD=30°,
∴BD=![]() AB=2;
AB=2;
当点D在线段BC的延长线上时,

∵∠DEC=30°,∠AED=60°,
∴∠AEC=30°,
∵△ABD≌△ACE,
∴∠ADB=∠AEC=30°,又∠B=60°,
∴∠BAD=90°,
∴BD=2AB=8,
∴BD为2或8时,∠DEC=30°;


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,设甲每天加工x个玩具:
(1)乙每天加工 个玩具(用含x的代数式表示);
(2)求甲乙两人每天各加工多少个玩具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC切⊙O于点C,AB过圆心O交⊙O于点B、D,且AC=BC,若⊙O的半径为2,图中阴影部分的面积为 _____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m.鸡场的面积能达到150m2吗?如果能,请你给出设计方案;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为64,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
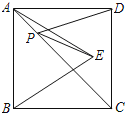
A.6B.8C.9D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与弧AB交于点D,以O为圆心,OC的长为半径作弧CE交OB于点E,若OA=6,∠AOB=120°,则图中阴影部分的面积为_________(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com