
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、数的开方法则及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:(1)原式=2+1+3+2+1
=9;
(2)原式=$\frac{a+1}{a-1}$-$\frac{a}{(a-1)^{2}}$•a
=$\frac{a+1}{a-1}$-$\frac{{a}^{2}}{{(a-1)}^{2}}$
=$\frac{{a}^{2}-1-{a}^{2}}{{(a-1)}^{2}}$
=$\frac{-1}{{(a-1)}^{2}}$,
当a=1-$\sqrt{2}$时,原式=$\frac{-1}{{(1-\sqrt{2}-1)}^{2}}$=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
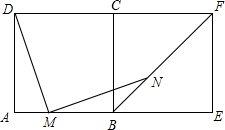 如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.
如图,正方形ABCD和正方形BEFC,M是AB上一动点,从A至B移动(不与A、B重合),DM⊥MN,交对角线BF于点N,探究DM和MN之间的数量关系,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15,15 | B. | 15,13 | C. | 15,12 | D. | 13,15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
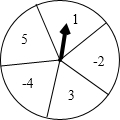 如图,有一个可以自由转动的转盘被平均分成五个扇形,五个扇形内部分别标有数字.1、-2、3、-4、5.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为m,n(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).请用列表或者画树状图的方法求出所有可能得到的点A的坐标,并求出点A在第一象限内的概率.
如图,有一个可以自由转动的转盘被平均分成五个扇形,五个扇形内部分别标有数字.1、-2、3、-4、5.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为m,n(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).请用列表或者画树状图的方法求出所有可能得到的点A的坐标,并求出点A在第一象限内的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
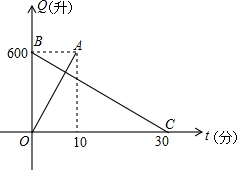 有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t(分)变化的函数关系.
有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t(分)变化的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com