
【题目】如图,以40m/s的速度将小球沿与地面成某一角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间(单位:s)之间具有函数关系h=20t﹣5t2.请解答以下问题:
(1)小球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)小球的飞行高度能否达到20.5m?为什么?
(3)小球从飞出到落地要用多少时间?
【答案】(1)小球的飞行1s和3s时,高度达到15 m;(2)小球的飞行高度不能达到20.5 m;(3)小球从飞出到落地要用4s.
【解析】
试题分析:(1)当h=15米时,15=20t﹣5t2,解方程即可解答;
(2)当h=20.5,得方程20.5=20t﹣5t2,解方程即可解答;
(3)当h=0时,0=20t﹣5t2,解方程即可解答.
解:(1)令h=15,得方程15=20t﹣5t2,
解这个方程得:t1=1,t2=3,
当小球的飞行1s和3s时,高度达到15 m;
(2)令h=20.5,得方程20.5=20t﹣5t2,
整理得:t2﹣4 t+4.1=0,
因为(﹣4)2﹣4×4.1<0,
所以方程无实数根,
所以小球的飞行高度不能达到20.5 m;
(3)小球飞出和落地时的高度都为0,令h=0,
得方程 0=20t﹣5t2,
解这个方程得:t1=0,t2=4,
所以小球从飞出到落地要用4s.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法正确的个数是( )
①a>0;②b>0;③c<0;④b2﹣4ac>0;⑤a+b+c=0.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(![]() )2+1=2 S1=
)2+1=2 S1=![]() ;
;
OA32=(![]() )2+1=3 S2=
)2+1=3 S2=![]() ;
;
OA42=(![]() )2+1=4 S3=
)2+1=4 S3=![]() …
…
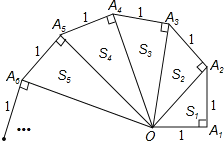
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com