
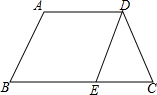
 如图,已知梯形ABCD中,AD∥BC,AB=DC,AB<AD,BC<2AD,DE∥AB,在以图中字母标注的点为起点和终点的有向线段中,将满足以下各题所列条件的所有有向线段用符号表示出来.
如图,已知梯形ABCD中,AD∥BC,AB=DC,AB<AD,BC<2AD,DE∥AB,在以图中字母标注的点为起点和终点的有向线段中,将满足以下各题所列条件的所有有向线段用符号表示出来.分析 (1)由AD∥BC,DE∥AB,可得四边形ABED是平行四边形,直接利用平行四边形的法则求解即可求得答案;
(2)易证得△DEC是等腰三角形,即可求得与有向线段$\overrightarrow{AB}$方向不同但长度相等的向量;
(3)由四边形ABED是平行四边形,直接利用平行四边形的法则,即可求得与有向线段$\overrightarrow{AD}$方向相反且长度相等的向量;
(4)由平行向量的知识,可求得与有向线段$\overrightarrow{AD}$方向相反且长度不等的向量;
(5)由平行向量的知识,可求得与有向线段$\overrightarrow{AD}$方向相同但长度不等的向量.
解答 解:(1)∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴与有向线段$\overrightarrow{AB}$方向相同且长度相等的是:$\overrightarrow{DE}$;
(2)∵梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C,
∵DE∥AB,
∴∠DEC=∠B,
∴∠DEC=∠C,
∴DE=DC,
∴与有向线段$\overrightarrow{AB}$方向不同但长度相等:$\overrightarrow{BA}$,$\overrightarrow{ED}$,$\overrightarrow{DC}$,$\overrightarrow{CD}$;
(3)∵四边形ABED是平行四边形,
∴与有向线段$\overrightarrow{AD}$方向相反且长度相等的是:$\overrightarrow{DA}$,$\overrightarrow{EB}$;
(4)与有向线段$\overrightarrow{AD}$方向相反且长度不等的有:$\overrightarrow{CB}$;
(5)与有向线段$\overrightarrow{AD}$方向相同但长度不等的是:$\overrightarrow{BC}$.
点评 此题考查了平面向量的知识、梯形的性质以及平行四边形的性质与判定.注意掌握平行四边形法则的应用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
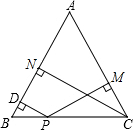 如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AB于点D,PM⊥AC于点M,CN为高,若AC=8,S△ABC=20,求PD+PM的值.
如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AB于点D,PM⊥AC于点M,CN为高,若AC=8,S△ABC=20,求PD+PM的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
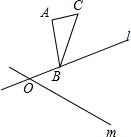 如图,直线1和m相交于点O
如图,直线1和m相交于点O查看答案和解析>>
科目:初中数学 来源: 题型:填空题
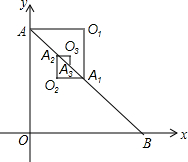 如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).
如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 电脑型号 | ① | ② | ③ |
| 工时(个) | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值(万元) | 0.4 | 0.3 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在⊙O中,AB=CD,则下列结论错误的是( )
如图,在⊙O中,AB=CD,则下列结论错误的是( )| A. | $\widehat{AB}=\widehat{CD}$ | B. | $\widehat{AC}$=$\widehat{BD}$ | C. | AC=BD | D. | AD=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com