
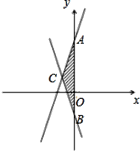
【题目】已知,直线 y=2x+3 与直线 y= ﹣ 2x ﹣ 1.
( 1 )求两直线与 y 轴交点A,B的坐标;
( 2 )求两直线交点 C 的坐标;
( 3 )求 △ ABC 的面积.
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
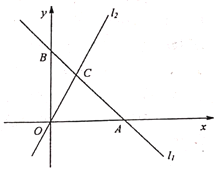
【题目】实践与探究
如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 坐标为
坐标为![]() 。直线
。直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,点
,点![]() 的横坐标为1。
的横坐标为1。
(1)求直线![]() 的解析式;
的解析式;
(2)若点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() 的面积是
的面积是![]() 面积的
面积的![]() ,求点
,求点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料1:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号.如:![]()
![]() ;
;
材料2: 配方法是初中数学思想方法中的一种重要的解题方法。配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题。它的应用非常广泛,在解方程、求最值、证明等式、化简根式、因式分解等方面都经常用到。
如:![]()
∵![]() ,∴
,∴![]() 即
即![]()
∴![]() 的最小值为1.
的最小值为1.
根据以上材料解决下列问题:
(1)填空:![]() =________________;
=________________;![]() =______________;
=______________;
(2)求![]() 的最小值;
的最小值;
(3)已知![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则![]() ;③ 若
;③ 若![]() ,则
,则![]() 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则![]() 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线:![]() 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
(1)求双曲线与抛物线的解析式;
(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
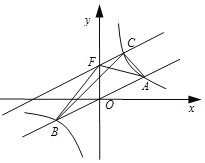
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com