练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】图中的小方格都是边长为1的正方形，△ABC的顶点和O点都在正方形的顶点上．

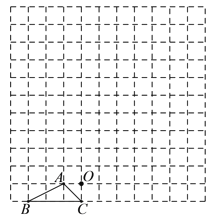
    （1）以点O为位似中心，在方格图中将△ABC放大为原来的2倍，得到△A1B1C1；

    （2）将△A1B1C1绕点B1顺时针旋转90°，画出旋转后得到的△A2B1C2；

    （3）在（2）的旋转过程中，点A1的运动路径长为 　，边A1C1扫过的区域面积为 　．

    【答案】（1）见详解；（2）见详解；（3）；

    【解析】

    （1）根据位似中心和位似比分别画出三个点，顺次连接即可；

    （2）根据旋转中心和旋转角度，分别找到，顺次连接即可；

    （3）分别在图中找到点A1的运动路径和A1C1扫过的区域面积，利用弧长公式和扇形的面积公式求解即可.

    （1）如图

    （2）如图

    （3）如图，点A1的运动路径为 ,A1C1扫过的区域面积通过转化为扇形与扇形之差.

    由勾股定理得 ，由图可知

    ∴

    A1C1扫过的区域面积为

    故答案为；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线，在四边形ABCD中，对角线BD是它的相似对角线，∠ABC=70°，BD平分∠ABC，那么∠ADC=____________度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为了测量山脚到塔顶的高度（即的长），某同学在山脚处用测角仪测得塔顶的仰角为，再沿坡度为的小山坡前进400米到达点，在处测得塔顶的仰角为.

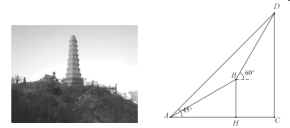
    （1）求坡面的铅垂高度（即的长）；

    （2）求的长.（结果保留根号，测角仪的高度忽略不计）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

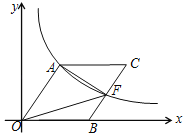
    【题目】如图，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，点A的横纵坐标之比为3：4，反比例函数y＝（k＞0）在第一象限内的图象经过点A，且与BC交于点F．

    （1）若OA＝10，求反比例函数解析式；

    （2）若点F为BC的中点，且△AOF的面积S＝12，求OA的长和点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

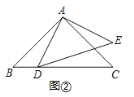
    【题目】（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，试探索线段BC，DC，EC之间满足的等量关系，并证明你的结论．

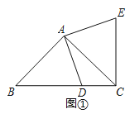
    （2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

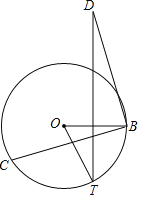
    【题目】如图，C为圆O上一动点（不与点B重合），点T为圆O上一动点，且∠BOT＝60°，将BC绕点B顺时针旋转90°得到BD，连接TD，当TD最大时，∠BDT的度数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝x2．

    （1）在抛物线上有一点A(1，1)，过点A的直线l与抛物线只有一个公共点，直接写出直线l的解析式；

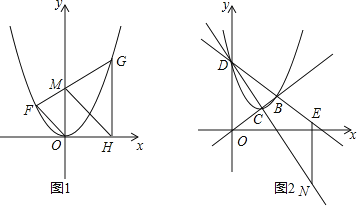
    （2）如图1，抛物线有两点F、G，连接FG交y轴于M，过G作x轴的垂线，垂足为H，连接HM、OF，求证：OF∥MH；

    （3）将抛物线y＝x2沿直线y＝x移动，新抛物线的顶点C，与直线的另一个交点为B，与y轴的交点为D，作直线x＝4与直线CD、BD交于点N、E，如图2，求EN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如下图，在△ABC中，∠ACB＝90°，D是AB的中点，以DC为直径的⊙O交△ABC的边于G，F，E点．求证：（1）∠A＝∠GEF；（2）△BDF≌FEC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

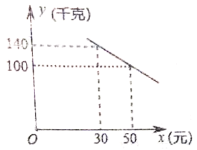
    【题目】我市某化工材料经销商购进一种化工材料若干千克，成本为每千克30元，物价部门规定其销售单价不低于成本价且不高于成本价的2倍，经试销发现，日销售量（千克）与销售单价（元）符合一次函数关系，如图所示.

    （1）求与之间的函数关系式，并写出自变量的取值范围；

    （2）若在销售过程中每天还要支付其他费用500元，当销售单价为多少时，该公司日获利最大？最大获利是多少元？

    查看答案和解析>>

    同步练习册答案